ДЛИНА СВОБОДНОГО ПРОБЕГА

ДЛИНА СВОБОДНОГО ПРОБЕГА

       

(средняя длина свободного пробега, l), средняя длина пути, проходимого ч-цей между двумя последоват. соударениями с др. ч-цами. Т. к. столкновения могут быть разного типа — упругие, неупругие, с возбуждением или ионизацией и т. д. (см. СТОЛКНОВЕНИЯ АТОМНЫЕ), соответственно различают Д. с. п. между столкновениями того или иного типа. Понятие «Д. с. п.» впервые появилось в кинетической теории газов. Если за 1 с молекула газа проходит в среднем путь v, испытывая при этом n упругих соударений с такими же молекулами и двигаясь в интервале между соударениями равномерно и прямолинейно, то l=v/n=1/(ns?2), где n — число молекул в ед. объёма (плотность газа), a — сечение эффективное молекулы. Для обычных мол. газов в норм. условиях l =10-5 см, что примерно в 100 раз больше ср. расстояния между молекулами. Понятие «Д. с. п.» в кинетич. теории газов было обобщено и для систем слабо взаимодействующих ч-ц, образующих газоподобные системы (электронный газ в металлах и ПП, нейтроны в слабо поглощающих средах и т. п.). В теории неравновесных процессов естественно возникает нек-рая величина размерности длины, к-рую возможно истолковать как Д. с. п. Она входит в выражения для коэфф. разл. явлений переноса.

Д. с. п. заряженных частиц (электронов и ионов). При классическом рассмотрении понятия эффективного сечения и Д. с. п. по отношению к упругим столкновениям заряж. ч-ц теряют смысл, т. к. вз-ствие ионов (эл-нов) с атомами (молекулами) может происходить и на расстоянии. В рамках квант. механики, рассматривая упругие вз-ствия заряж. ч-ц, получают конечные значения для эфф. поперечного сечения и, следовательно, для Д. с. п., если вз-ствие убывает быстрее, чем 1/r3. В плазме можно определить Д. с. п. для упругих вз-ствий, считая, что радиус действия поля рассеивающих центров не превышает дебаевского радиуса экранирования. По отношению к неупругим процессам Д. с. п. определяется ср. расстоянием, к-рое проходит ион (эл-н) при данной скорости, прежде чем примет участие в процессе.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ДЛИНА СВОБОДНОГО ПРОБЕГА

(точнее, средняя длина свободного пробега) - ср. расстояние, к-рое проходит частица между двумя последоват. столкновениями. Д. с. п.- важное понятие кинетической теории газов, введённое P. Клаузиусом (R. Clausius) в 1858.

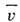Д. с. п. равна , где - ср. скорость молекул, - ср. время между столкновениями, причём , - частота столкновений, т. е. ср. число столкновений, испытываемых молекулой за единицу времени в единице объёма. Следовательно, . Для газа упругих сфер радиуса а частота столкновений , где п - число молекул в единице объёма,- полное эфф. сечение столкновения,.

В общем случае частота столкновений равна , где и - модуль относит. скорости,

- полное эфф. сечение столкновений,

угл. скобки означают усреднение по Максвелла распределению относительных скоростей с приведённой массой -дифференц. эфф. сечение столкновения. При вычислении кинетических коэф. оказываются существенными т. н. транспортные Д. с. п. Напр., для диффузии вводят транспортное эфф. сечение

а для вязкости

Понятие Д. с. п. удобно для качеств. рассмотрения явлений переноса в газах, оно обобщено на случай систем слабовзаимодействующих частиц: электронный газ в металлах и полупроводниках, нейтроны в слабопоглощающих средах и т. п.

Лит.: Чепмен С., Каулинг Т., Математическая теория неоднородных газов, пер. с англ., M., 1960, гл.5; Ферцигер Д да., Капер Г., Математическая теория процессов переноса в газах, пер. с англ., M., 1976, гл. 2, 14. Д. H. Зубарев.

Д. с. п. заряженных частиц (электронов и ионов). При классич. рассмотрении понятия полного эффективного сечения и Д. с. п. по отношению к упругим столкновениям заряж. частиц теряют смысл, поскольку за-ряж. частицы взаимодействуют между собой на сколь угодно больших расстояниях r. Квантовая механика, основываясь на соотношениях неопределённостей, даёт конечное значение для 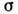и l, если взаимодействие убывает быстрее, чем 1/r³. В плазме существен эффект экранирования кулоновского поля заряда на расстояниях, определяемых дебаевским радиусом зкранирования.

В плазме с электронной темп-рой Т _е и плотностью электронов N (плотность ионов при этом равна N/Z_i, где Z_i - ср. заряд ионов) Д. с. п. электронов по отношению к электрон-электронным столкновениям равна , здесь е - заряд электрона и L_e - к улоновский логарифм, зависящий от Т _е и дебаевского радиуса. Д. с. п. электронов по отношению к электрон-ионным столкновениям в Z_i раз меньше и составляет 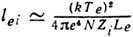Д. с. п. ионов по отношению к ионионным столкновениям: , где T_i - ионная темп-pa, L_i - кулоновский логарифм с ионными величинами вместо электронных.

С помощью Д. с. п. производятся аналитич. оценки кинетических коэф. газов и плазмы.

Лит.: Смирнов Б. M., Физика слабоионизованного газа, M., 1972; Лифшиц E. M., Питаевский Л. П., Физическая кинетика, M., 1979. Л. П. Пресняков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.