- ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ
- ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ
-
раздел газовой динамики, в к-ром при изучении течения газа низкой плотности учитывается его дискретная мол. структура. Методы Д. р. г., основанные на молекулярно-кинетич. теории газов, применяются для определения теплового и силового воздействия газа на поверхности летат. аппаратов, движущихся на больших высотах, а также при расчёте движения газов в вакуумных системах, истечения струй в пр-во с низким давлением и в задачах мол. физики.Критерием, характеризующим степень разреженности движущегося газа, явл. число Кнудсена Kn»l/L, где l — ср. длина свободного пробега молекул в газе, L — характерный размер течения. Предположение о сплошности среды, лежащее в основе теор. методов гидроаэромеханики и газовой динамики, строго выполняется лишь в предельном случае Kn®0, а практически оно оказывается справедливым уже при Kn<10-3.В другом предельном случае Kn®? существенную роль играют только столкновения молекул газа с обтекаемыми телами, а роль межмол. столкновений незначительна. Поэтому набегающий на поверхность тела поток молекул и поток молекул, отражённый от поверхности, рассматриваются как невзаимодействующие. При этом из ур-ний движения молекул можно определить баланс между приносимыми к поверхности и уносимыми от неё потоками массы, импульса и энергии, если известен механизм вз-ствия молекул газа с поверхностью. Такая схема позволяет с достаточной для практики точностью рассчитать аэродинамич. хар-ки разл. тел уже при Kn>1. Режим течения, для к-рого справедливы указанные предположения, наз. с в о б о д н о м о л е к у л я р н ы м. Одной из приближённых схем описания вз-ствия молекул газа с тв. поверхностью при свободномол. течении является т. н. зеркально-диффузная схема, согласно к-рой часть молекул отражается диффузно в соответствии с законом косинуса (Ламберта законом), а остальные молекулы — зеркально, т. е. по закону — угол падения равен углу отражения. Отношение кол-ва диффузно рассеянных молекул к общему их числу определяет степень диффузности f рассеяния (при f=0 происходит только зеркальное отражение, при f=1 — только диффузное). Обмен энергией при вз-ствии молекул с тв. поверхностью характеризуют коэфф. аккомодации а, определяющим изменение энергии молекулы после её отражения от поверхности. Значения а меняются от 0 до 1. Если после отражения энергия молекулы не изменилась, то a=0, если же ср. энергия отражённых молекул, характеризующая темп-ру газа, соответствует темп-ре стенки, то a=1. В общем случае коэффициенты f и a зависят от скорости столкновения молекул с поверхностью, от материала и темп-ры этой поверхности, от степени её гладкости, наличия на ней адсорбиров. молекул газа и т. д. Переход от течения сплошной среды (Kn®0) к свободномол. течению (Kn®?), напр. при увеличении высоты полёта, осуществляется через ряд промежуточных режимов течения разреженного газа. Каждому из них соответствует определ. диапазон конечных значений числа Kn. В переходном режиме оказывается важным как учёт межмол. столкновений, так и столкновений молекул газа с поверхностью обтекаемого тела. Для этого режима течения характерно проявление ряда сложных неравновесных мол. процессов, строгое теор. описание к-рых в промежуточной области чисел Kn представляет огромные матем. трудности, связанные с решением интегродифф. ур-ния Больцмана для изменения во времени и в пр-ве ф-ции распределения молекул по скоростям (см. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ). Поэтому широко применяются приближённые теор. методы, позволяющие распространить теор. модели свободномол. течения и течения сплошной среды на режимы, соответствующие промежуточной области значения чисел Kn, близких к предельным. Так, разработаны приближённые методы расчёта аэродинамич. хар-к тел в случае, когда учитываются лишь однократные столкновения падающих на поверхность и отражённых от неё молекул (режим, примыкающий к свободномол. течению). Ур-ния газовой динамики сплошной среды применяют и при Kn>10-3, но с новыми граничными условиями, учитывающими характерные для течения разреженного газа условия «скольжения» и «скачка темп-ры». Первое условие состоит в том, что параллельная стенке составляющая скорости газа на самой стенке отличается от нуля, а второе учитывает отличие темп-ры газа вблизи стенки от темп-ры стенки. Различные, постепенно сменяющие друг друга режимы течения — от свободномол. до континуального — наблюдаются в классич. задаче Д. р. г. об обтекании газом плоской полубесконечной пластинки (рис. 1).При рассмотрении сверхзвук. обтекания затупленных тел в режимах, примыкающих к течению сплошной среды, число Kn определяют как отношение длины свободного пробега ls молекул в сжатом слое газа за отошедшей от тела ударной волной к характерному размеру тела. В случае полёта сферич. тела радиусом R»1 м со скоростью v»10 км/с и постепенном увеличении высоты полёта (уменьшении числа Kn=ls/R) можно выделить след. режимы, а) При Kn<0,5•10-3 (что соответствует выcoтaм=70 км) течение явл. континуальным. Ударная волна толщиной порядка неск. ls и вязкий пограничный слой на поверхности сферы разделены областью, где вязкость газа несущественна.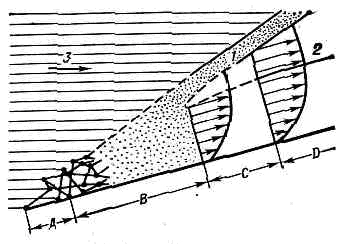 Рис. 1. Схема развития течения газа около плоской полубесконечной тонкой пластины, обтекаемой сверхзвук. потоком под углом атаки: А — область свободномол. течения с однократными столкновениями; В — область с многократными столкновениями; С — область течения со скольжением; D — континуум; 1 — ударная волна; 2 — граница пограничного слоя; 3 — макроскопич. движение потока молекул (масштабы зон и областей не соблюдены).б) При Kn»0,5•10-2 (увеличение высот до 85 км) отошедшая ударная волна и пограничный слой на теле утолщаются, а затем смыкаются. Перед сферой образуется сплошная область (рис. 2, а). Уменьшение числа столкновений между молекулами в сжатом слое приводит к запаздыванию в установлении равновесия по колебат. степеням свободы молекул.
Рис. 1. Схема развития течения газа около плоской полубесконечной тонкой пластины, обтекаемой сверхзвук. потоком под углом атаки: А — область свободномол. течения с однократными столкновениями; В — область с многократными столкновениями; С — область течения со скольжением; D — континуум; 1 — ударная волна; 2 — граница пограничного слоя; 3 — макроскопич. движение потока молекул (масштабы зон и областей не соблюдены).б) При Kn»0,5•10-2 (увеличение высот до 85 км) отошедшая ударная волна и пограничный слой на теле утолщаются, а затем смыкаются. Перед сферой образуется сплошная область (рис. 2, а). Уменьшение числа столкновений между молекулами в сжатом слое приводит к запаздыванию в установлении равновесия по колебат. степеням свободы молекул. Рис. 2. Фотография обтекания сферы диам. 15 мм: а — в разреженном газе при числах Маха М=3,7 и Kn=2,5•10-2; б — в сплошной среде.Граничные условия на поверхности сферы соответствуют скольжению молекул и скачку темп-ры. Течение разреженного газа, соответствующее диапазону 0,5•10-3Отошедшая ударная волна не формируется. г) При дальнейшем увеличении числа Kn механизм обтекания целиком определяется дискр. структурой среды. Время пребывания каждой молекулы вблизи тела характеризуется всего неск. столкновениями. Дальнейшее уменьшение плотности газа приводит к свободномол. течению, граница к-рого в данном случае соответствует высоте »200 км.
Рис. 2. Фотография обтекания сферы диам. 15 мм: а — в разреженном газе при числах Маха М=3,7 и Kn=2,5•10-2; б — в сплошной среде.Граничные условия на поверхности сферы соответствуют скольжению молекул и скачку темп-ры. Течение разреженного газа, соответствующее диапазону 0,5•10-3Отошедшая ударная волна не формируется. г) При дальнейшем увеличении числа Kn механизм обтекания целиком определяется дискр. структурой среды. Время пребывания каждой молекулы вблизи тела характеризуется всего неск. столкновениями. Дальнейшее уменьшение плотности газа приводит к свободномол. течению, граница к-рого в данном случае соответствует высоте »200 км.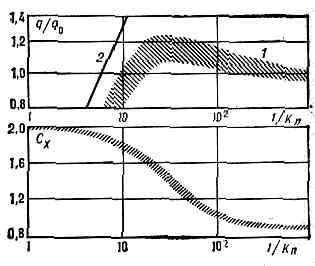 Рис. 3. Изменение коэфф. лобового сопротивления сферы Сх и относительного теплового потока q/q0 в передней критич. точке сферы в промежуточной области чисел Kn: q0 — тепловой поток, рассчитанный по теории пограничного слоя (Kn®0); 1 — эксперимент для сильного охлаждения сферы при М>5; 2 — расчёт для сильно охлаждённой сферы при Kn®?, a=1.В рассмотренном диапазоне чисел Kn величины теплового потока q и коэфф. сопротивления Сх изменяются от значений, соответствующих течению сплошной среды, до значений, соответствующих свободномол. режиму, как это показано на рис. 3. С помощью методов Д. р. г. рассматриваются также задачи исследования хар-к течения в отверстиях, вакуумных трубопроводах и каналах. Важным для техн. приложений явл. изучение законов уменьшения пропускной способности каналов разл. форм и размеров при увеличении числа Kn. Исследуются эффекты разреженности при течении газов в соплах и струях двигателей, работающих на больших высотах.Ввиду чрезвычайных матем. трудностей теор. методов исследования Д. р. г., важное значение имеет эксперимент (см. АЭРОДИНАМИЧЕСКИЕ ИЗМЕРЕНИЯ). Эксперим. исследования течений разреженного газа проводятся на спец. вакуумных аэродинамических трубах, оборудованных мощными системами откачки, включающими форвакуумные, пароструйные и криогенные насосы. Применяемые на этих установках методы обладают рядом специфич. особенностей по сравнению с методами, используемыми в обычных аэродинамич. установках. Малые плотности газа, низкие по абс. величинам, тепловые потоки и аэродинамич. силы требуют применения высокочувствит. датчиков и приборов, а также принципиально новых физ. методов диагностики. Так, широко используется электронно-пучковая диагностика, основанная на регистрации интенсивности видимого, УФ и рентг. излучения молекул газа, возбуждаемых пучком быстрых (10—30 кэВ) эл-нов. Этот метод позволяет проводить визуализацию течения, а также измерять локальные величины плотности, темп-ры, скорости потока, а также концентрации компонентов разреженной смеси газов.
Рис. 3. Изменение коэфф. лобового сопротивления сферы Сх и относительного теплового потока q/q0 в передней критич. точке сферы в промежуточной области чисел Kn: q0 — тепловой поток, рассчитанный по теории пограничного слоя (Kn®0); 1 — эксперимент для сильного охлаждения сферы при М>5; 2 — расчёт для сильно охлаждённой сферы при Kn®?, a=1.В рассмотренном диапазоне чисел Kn величины теплового потока q и коэфф. сопротивления Сх изменяются от значений, соответствующих течению сплошной среды, до значений, соответствующих свободномол. режиму, как это показано на рис. 3. С помощью методов Д. р. г. рассматриваются также задачи исследования хар-к течения в отверстиях, вакуумных трубопроводах и каналах. Важным для техн. приложений явл. изучение законов уменьшения пропускной способности каналов разл. форм и размеров при увеличении числа Kn. Исследуются эффекты разреженности при течении газов в соплах и струях двигателей, работающих на больших высотах.Ввиду чрезвычайных матем. трудностей теор. методов исследования Д. р. г., важное значение имеет эксперимент (см. АЭРОДИНАМИЧЕСКИЕ ИЗМЕРЕНИЯ). Эксперим. исследования течений разреженного газа проводятся на спец. вакуумных аэродинамических трубах, оборудованных мощными системами откачки, включающими форвакуумные, пароструйные и криогенные насосы. Применяемые на этих установках методы обладают рядом специфич. особенностей по сравнению с методами, используемыми в обычных аэродинамич. установках. Малые плотности газа, низкие по абс. величинам, тепловые потоки и аэродинамич. силы требуют применения высокочувствит. датчиков и приборов, а также принципиально новых физ. методов диагностики. Так, широко используется электронно-пучковая диагностика, основанная на регистрации интенсивности видимого, УФ и рентг. излучения молекул газа, возбуждаемых пучком быстрых (10—30 кэВ) эл-нов. Этот метод позволяет проводить визуализацию течения, а также измерять локальные величины плотности, темп-ры, скорости потока, а также концентрации компонентов разреженной смеси газов.Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
.
ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ — раздел механики газов, в к ром изучаются явления, требующие учёта молекулярной структуры, привлечения представлений и методов кинетической теории газов. Толчком к бурному росту исследований в этой области и образованию на стыке газовой динамики и … Физическая энциклопедия
ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ — раздел газовой динамики, в к ром при изучении течения газа низкой плотности учитывается его дискретная мол. структура. Методы Д. р. г , основанные на молекулярно кинетич. теории газов, применяются для определения теплового и силового воздействия… … Естествознание. Энциклопедический словарь
РАЗРЕЖЕННЫХ ГАЗОВ ДИНАМИКА — (см. ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
Разреженных газов динамика — раздел газовой динамики, изучающий явления, требующие учёта молекулярной структуры газа и, следовательно, привлечения представлений и методов кинетической теории газов. Классическая газовая динамика справедлива когда Кнудсена число Kn < < 1, то… … Энциклопедия техники
АЭРОДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ — (см. ДИНАМИКА РАЗРЕЖЕННЫХ ГАЗОВ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
Аэродинамика разреженных газов — раздел механики газов, в котором для описания движения газов необходимо учитывать их молекулярное строение. Методы А. р. г. широко применяют при определении аэродинамического нагрева (См. Аэродинамический нагрев) приземляющихся… … Большая советская энциклопедия
разреженных газов динамика — Течение Куэтта. разреженных газов динамика, раздел газовой динамики, изучающий явления, требующие учёта молекулярной структуры газа и, следовательно, привлечения представлений и методов кинетической теории газов.Классическая газовая динамика… … Энциклопедия «Авиация»
разреженных газов динамика — Течение Куэтта. разреженных газов динамика, раздел газовой динамики, изучающий явления, требующие учёта молекулярной структуры газа и, следовательно, привлечения представлений и методов кинетической теории газов.Классическая газовая динамика… … Энциклопедия «Авиация»
Динамика — (Dynamics) Содержание Содержание 1. в разных науках В физике В астрономии В науках о Земле В биологии В технике В музыке 2. Динамика в физике 3. Ряды динамики 4. Газовая динамика Динамика – это состояние движения, ход развития, изменение… … Энциклопедия инвестора
ГАЗОВАЯ ДИНАМИКА — раздел гидроаэромеханики, в к ром изучается движение сжимаемых сплошных сред (газа, плазмы) и их вз ствие с тв. телами. Как часть физики, Г. д. связана с термодинамикой и акустикой. Св во сжимаемости состоит в способности в ва изменять свой… … Физическая энциклопедия
