УРОВНИ ЭНЕРГИИ

УРОВНИ ЭНЕРГИИ

       

возможные значения энергии квант. систем (атомов, молекул, ат. ядер и т. д.), состоящих из микрочастиц и подчиняющихся законам квантовой механики. Внутр. энергия квант. систем может принимать только определённые дискр. значения: ?0, ?1, ?2, ... , (?0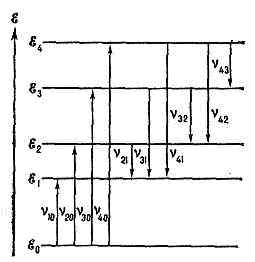

Графически эти состояния можно изобразить по аналогии с потенц. энергией тела, поднятого на разл. высоты (уровни), в виде диаграммы У. э. (рис.). Каждому значению энергии соответствует горизонтальная линия, проведённая (в определ. масштабе) на высоте ?i (i=0, 1, 2, ...). Совокупность У. э. рассматриваемой квант. системы образует её энергетический спектр. Нижний уровень ?0, соответствующий наименьшей возможной энергии системы, наз. основным, все остальные — ?1, ?2, ...— возбуждёнными, т. к. для перехода на них необходимо возбудить систему — сообщить ей энергию.

Квантовые переходы между У. э. обозначают на диаграммах вертикальными (или наклонными) прямыми, соединяющими соответствующие пары У. э. На рис. показаны излучат. переходы с частотами nik, удовлетворяющими условию частот: hnik=?i-?k; безызлучат. переходы часто обозначаются волнистыми линиями. Направление перехода указывают стрелкой: стрелка, направленная вниз, соответствует процессу испускания фотона, стрелка в обратном направлении — процессу поглощения фотона с энергией hnik. Дискр. энергетич. спектру соответствуют дискр. спектры поглощения и испускания (см. СПЕКТРЫ ОПТИЧЕСКИЕ).

Для квант. системы, имеющей в определ. диапазонах значений энергии непрерывный энергетич. спектр, на диаграмме получаются непрерывные последовательности У. э. в соответствующих диапазонах. Напр., для атома Н такая непрерывная последовательность имеет место при ? >??, где ?? — граница ионизации (см. рис. 1, б в ст. (см. АТОМ)), а для эл-на в кристалле получается чередование разрешённых и запрещённых энергетич. зон (см. ДИЭЛЕКТРИКИ, ПОЛУПРОВОДНИКИ). При излучат. квант. переходах между дискр. У. э. и У. э., относящимися к непрерывной последовательности, а также между непрерывными последовательностями У. э. получаются сплошные спектры поглощения и испускания.

Важной хар-кой У. э. являются их ширины (Г), связанные с временем жизни (t) квант. системы на уровне Г=1/t. У. э. тем уже, чем больше время жизни, в согласии с неопределённостей соотношением для энергии и времени (см. ШИРИНА УРОВНЯ).

При рассмотрении У. э. квант. систем значения энергии принято отсчитывать от осн. уровня. Наряду со шкалой энергий, обычно выражаемых в эВ (а для ат. ядер в МэВ или кэВ), в спектроскопии применяют пропорциональные ей шкалы частот n=?/h (в радиоспектроскопии) и волн. чисел v/c=?/hc (в оптич. спектроскопии); 1 эВ соответствует 2,4180•1014 Гц и 8065,5 см-1. В рентгеновской спектроскопии применяют ед. энергии ридберг: 1 Ry=13,606 эВ.

В оптич. спектроскопии часто применяют термин «спектральный терм», подразумевая под ним значение Т=-?/hc, отсчитываемое для атомов от границы ионизации и выражаемое в см-1.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

УРОВНИ ЭНЕРГИИ

- возможные значения энергии квантовых систем (атомов, молекул, кристаллов атомных ядер и т. д.), состоящих из микрочастиц и подчиняющихся законам квантовой механики. Внутр. энергия квантовых систем может принимать только определ. дискретные значения: 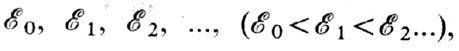соответствующие устойчивым (стационарным) состояниям системы. Графически эти состояния можно изобразить по аналогии с потенц. энергией тела, поднятого на разл. высоты (уровни), в виде диаграммы У. э. (рис.). Каждому значению энергии соответствует горизонтальная линия, проведённая (в определ. масштабе) на высоте 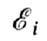(i=0, 1, 2, ...). Совокупность У. э. рассматриваемой квантовой системы образует её энергетический спектр. Ниж. уровень 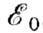, соответствующий наим. возможной энергии системы, наз. основным, все остальные- 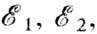...- возбуждёнными, т. к. для перехода из них необходимо возбудить систему-сообщить ей энергию.

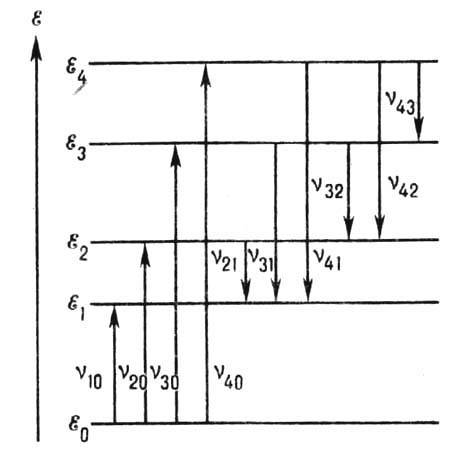
Квантовые переходы между У. э. обозначают на диаграммах вертикальными (или наклонными) прямыми, соединяющими соответствующие пары У. э. На рис. показаны излучат, переходы с частотами v_ik, удовлетворяющими условию частот: 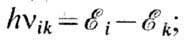безызлучат. переходы часто обозначаются волнистыми линиями. Направление перехода указывают стрелкой: стрелка, направленная вниз, соответствует процессу испускания фотона, стрелка в обратном направлении - процессу поглощения фотона с энергией 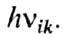Дискретному энергетич. спектру соответствуют дискретные спектры поглощения и испускания (см. Спектры оптические).

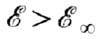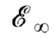Для квантовой системы, имеющей в определ. диапазонах значений энергии непрерывный энергетич. спектр, диаграмма выглядит в виде непрерывных последовательностей У. э. в соответствующих диапазонах. Напр., для атома Н такая непрерывная последовательность имеет место при , где -граница ионизации (рис. 1, б к ст. Атом), а для электрона в кристалле получается чередование разрешённых и запрещённых энергетич. зон (см. Диэлектрики, Полупроводники). При излучательных квантовых переходах между дискретными У. э. и У. э., относящимися к непрерывной последовательности, а также между непрерывными последовательностями У. э. получаются сплошные спектры поглощения и испускания.

Важной характеристикой У. э. являются их ширины (Г), связанные с временем жизни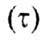квантовой системы на уровне: 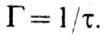У. э. тем уже, чем больше время жизни, в согласии с неопределённостей соотношением для энергии и времени (см. Ширина уровня).

При рассмотрении У. э. квантовых систем значения энергии принято отсчитывать от осн. уровня. Наряду со шкалой энергий (обычно выражаемых в эВ, для атомных ядер - в МэВ или кэВ) в спектроскопии применяют пропорциональные ей шкалы частот 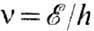(в радиоспектроскопии) и волновых чисел 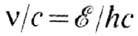(в оптич. спектроскопии); 1 эВ соответствует 2,4180-10¹⁴ Гц и 8065,5 см ^-1. В рентгеновской спектроскопии применяют единицу энергии ридберг; 1 Ry=13,606 эВ.

В оптич. спектроскопии часто употребляют термин "спектральный терм", подразумевая под ним значение 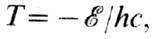отсчитываемое для атомов от границы ионизации и выражаемое в см ^-1.

Лит. см. при статьях Атом, Молекула, Твёрдое тело, Ядро атомное. • М. А. Елъяшевич.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.