ЭЛАСТОСОПРОТИВЛЕНИЕ

ЭЛАСТОСОПРОТИВЛЕНИЕ

- изменение уд. электросопротивления на единицу деформации (см. Тензорезистив-ный эффект):

Здесь r-сопротивление в отсутствие деформации,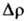- изменение r при деформации, 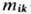-безразмерный тензор Э. 4-го ранга, 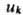-тензор деформации 2-го ранга. Относит. изменение уд. сопротивления деформированного кристалла в линейном по деформации приближении можно записать в виде где 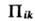-тензор пьезосопротивления 4-го ранга, Xi- тензор механич. напряжения 2-го ранга, связанный с тензором деформации 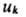(через тензор модулей упругости С _ik )соотношением

Компоненты тензора Э.

Так же, как и компоненты П _ik, компоненты 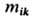образуют шестимерную матрицу. На основании (3) для кристаллов кубич. симметрии связь между коэф. пьезосопротивления и Э. имеет вид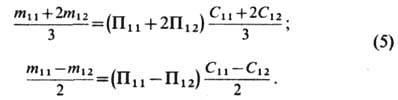

Соотношения (5) позволяют определить коэф. Э., измеряя коэф. пьезосопротивления. Вместо упругих постоянных 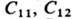можно пользоваться т. н. константами жёсткости 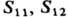(приводимыми обычно в таблицах):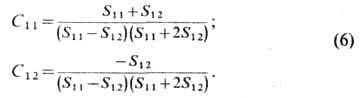

Если осн. минимумы энергии зоны проводимости кристалла (см. Зонная теория )расположены на осях [100] (что имеет место в h-Si), то

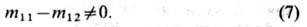Если осн. минимумы находятся на осях [111] (n-Ge), то

Лит.:Herring C., Transport properties of many-valley semiconductor, "Bell System Techn. Journal", 1955, v. 34, p. 237; Вир Г. Л., Пикус Г. E., Симметрия и деформационные эффекты в полупроводниках, M., 1972; Баранский П. И., Клочков В. П., Поты-кевич И. В., Полупроводниковая электроника, К., 1975.

П. И. Баранский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.