ФЕРМИ-ПОВЕРХНОСТЬ

ФЕРМИ-ПОВЕРХНОСТЬ

- изоэнергетич. поверхность в пространстве квазиимпульсов (p -пространстве), соответствующая фермы-энергии:

Здесь -дисперсии закон электрона проводимости; s- номер энергетич. зоны (см. Зонная теория). Ф.-п. отделяет при темп-ре Т=0 К занятые электронами проводимости состояния от свободных. Изображая Ф.-п., можно ограничиться одной ячейкой p -пространства (1-й Бриллю-эна зоной), т. к. в ней расположены концы векторов р, описывающие все неэквивалентные состояния. Но можно использовать расширенное (бесконечное) p -пространство, в к-ром каждая изоэнергетич. поверхность (и Ф.-п. тоже) периодична с периодом 2pbh, где b- произвольный вектор обратной решётки. Если Ф.-п. полностью умещается в одной ячейке p -пространства, то такую поверхность наз. з а м к н у т о й. Если Ф.-п. пересекает границы ячейки p -пространства, её наз. о т к р ы т о й. При использовании расширенного p -пространства замкнутая Ф.-п. бесконечно повторяется из ячейки в ячейку, а открытая проходит через всё p -пространство. Ф.-п. может быть открыта в одном, двух и трёх измерениях (рис. 1, 2, 3).

Рис. 1. Поверхность Ферми графита.

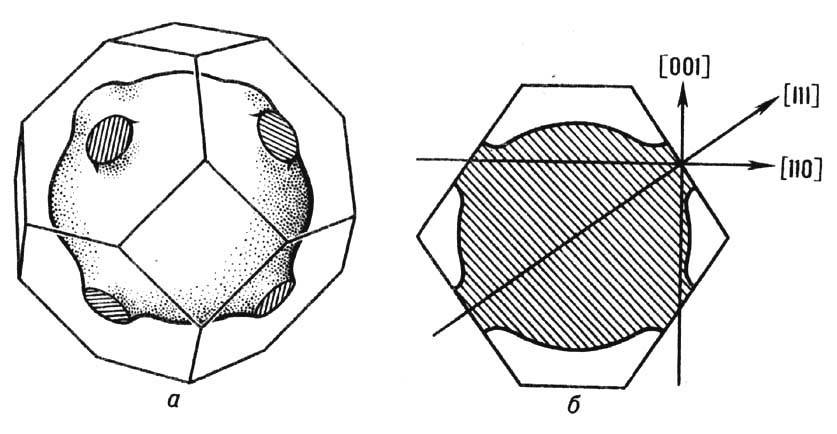
Рис. 2. а- Открытая поверхность Ферми Аu, Сu, Ag; б- сечение её плоскостью [110], видны откры тые направления.

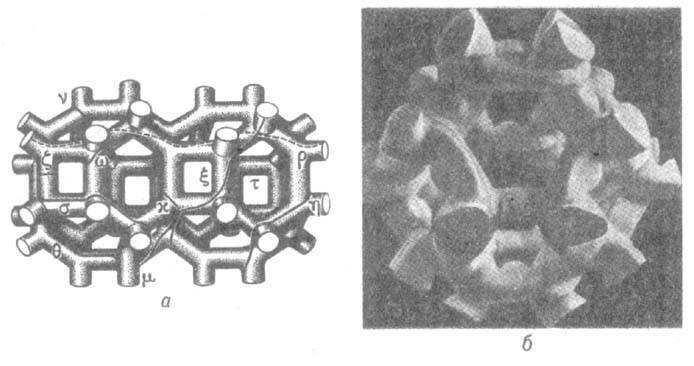
Рис. 3. а- Открытая электронная поверхность Ферми Рb; б- та же поверхность в одной ячейке обратной решётки.

У большинства металлов имеется неск. частично заполненных энергетич. зон. Поэтому, как правило, Ф.-п. имеет неск. полостей (к а р м а н о в, д о л и н), из к-рых одни могут быть открытыми, а другие замкнутыми. Замкнутая Ф.-п. может окружать область p -пространства, где 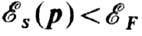; тогда при Т=0. К все состояния внутри Ф.-п. заняты. Такая Ф.-п. наз. э л е к т р о н н о й. Если внутри Ф.-п. имеются состояния с 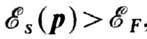, то при Т=0К они свободны, а Ф.-п. наз. д ы р о ч н о й. Нормаль к Ф.-п. есть скорость электрона 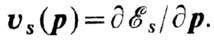У электронных Ф.-п. векторы скорости (нормали) направлены вовне поверхностей, у дырочных-внутрь.

Объём одной полости замкнутой Ф.-п. или часть объёма открытой Ф.-п. приходящаяся на одну ячейку p -пространства, с точностью до численного множителя совпадает с плотностью n_s электронов проводимости, принадлежащих s -й зоне:

Для дырочной Ф.-п. её объём принято связывать с плотностью n'_s дырок - плотностью свободных состояний в зоне:

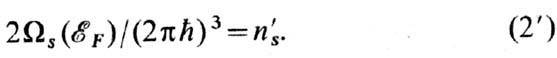
Особый класс составляют компенсированные металлы (Be, Bi), у к-рых объёмы электронных и дырочных полостей Ф.-п. равны, т. е. равны плотности электронов и дырок. Если Ф.-п.- сфера (К, Na, Rb, Cs), то её радиус равен

у эллипсоидальной Ф.-п. (Bi) размеры осей эллипсоида пропорциональны n^1/3.

Вычисление формы Ф.-п. конкретного металла пока неосуществимо, поэтому определение формы Ф.-п. производится по эксперим. данным. С разл. степенью точности известны Ф.-п. всех металлов и многих интерметаллических соединений. При этом используется тот факт, что большинство термодинамич., кинетич., акустич. и др. свойств металлов обусловлено электронами, занимающими состояния вблизи Ф.-п. В результате характеристики металла оказываются связанными с геом. характеристиками Ф.-п. (формой, кривизной, площадью сечений и др.). Так, сильная анизотропия магнетосопротивления указывает на открытость Ф.-п., знак постоянной Холла (см. Холла эффект )определяет характер Ф.-п. (электронная или дырочная), осцилляции магн. восприимчивости в сильных магн. полях ( де Хааза - ван Альфена эффект )позволяют определить площадь экстремального сечения Ф.-п.; поверхностный импеданс в условиях аномального скин-эффекта- ср. кривизну Ф.-п.; квантовый циклотронный резонанс- площадь всех (а не только экстремальных) сечений Ф.-п. и т. д.

Задача восстановления формы Ф.-п. по эксперим. данным не может быть решена без привлечения теоретич. моделей. Чаще всего применяют либо приближение (модель) почти свободных электронов, либо приближение сильно связанных электронов. Обе модели используют соображения симметрии, позволяющие определить общие контуры Ф.-п. Приближение почти свободных электронов предполагает, что вся анизотропия Ф.-п.- результат периодичности кристалла, В нулевом приближении Ф.-п.- совокупность сфер радиуса p_F с центрами в точках p -пространства p=2phb эквивалентных центру первой зоны Бриллюэна. Учёт взаимодействия электронов с кристал-лич. решёткой сводится к снятию вырождения (если диаметр сферы больше размера 1-й зоны Бриллюэна) и приводит к перестройке Ф.-п. (напр., возникают открытые поверхности). Получающиеся т. о. формы Ф.-п. многообразны, хотя и составлены из "обрезков" сфер.

Модель сильно связанных электронов использует разложение энергии электрона в решётке в ряд Фурье, а приближение состоит в том, что применяется не весь ряд, а лишь неск. его членов, обладающих всеми элементами симметрии кристалла.

Фазовый переход в металле сопровождается изменением его Ф.-п. Так, при переходе из парамагнитного в ферро-магн. состояние (см. Магнитный фазовый переход )происходит расщепление Ф.-п. на две - для электронов с различно направленными спинами.

Внеш. воздействие на металл может привести к изменению геометрии Ф.-п.: может возникнуть или исчезнуть полость Ф.-п. и (или) разорваться либо образоваться перемычка у Ф.-п. При этом электронные характеристики металла обнаруживают аномалии, называемые электронным топологическим переходом в нормальном металле.

Лит.: Крэкнелл А., Уонг К., Поверхность Ферми, пер. с англ., М., 1978; см. также лит. при ст. Металлы.

М. И. Каганов, Э. М. Эпштейн.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.