ТЕРМОДИНАМИКА НЕРАВНОВЕСНЫХ ПРОЦЕССОВ

ТЕРМОДИНАМИКА НЕРАВНОВЕСНЫХ ПРОЦЕССОВ

-общая теория макроскопич. описания термодинамически неравновесных процессов. Её наз, также н е р а вн о в е с н о й т е р м о д и н а м и к о й или т ер м о д и н а м и к о й н е о б р а т и м ы х п р о ц е с с о в.

Впервые термодинамич, соображения были применены к необратимым процессам В. Томсоном (Кельвином) в 1854. Последоват. изучение неравновесных процессов термодинамич. методами началось с работ Л. Онсагера, установившего в 1931 соотношения взаимности для коэф. феноменологич. законов, к-рым подчиняются необратимые процессы. Как самостоят. наука Т. н. п. стала развиваться в работах Дж. Мейкснера, И. Пригожина и С. де Гроота.

Классич. термодинамика даёт полное количеств. описание равновесных (обратимых) процессов, поэтому её иногда называют термостатикой. Для неравновесных процессов она устанавливает лишь неравенства, к-рые указывают направление этих процессов (напр., Клаузиуса неравенство). Осн. задача Т. н. п.- количеств. изучение неравновесных процессов для. состояний, не сильно отличающихся от равновесных, в частности определение скоростей неравновесных процессов в зависимости от внеш. условий. В Т. н. п. системы, в к-рых протекают неравновесные процессы, рассматривают как непрерывные среды, а их параметры состояния-как полевые переменные, т. е. непрерывные ф-ции координат и времени. Для макроскопич. описания неравновесных процессов систему представляют состоящей из элементарных объёмов (физически бесконечно малых элементов среды), к-рые всё же настолько велики, что содержат очень большое число частиц. Состояние каждого выделенного элемента среды характеризуется темп-рой, плотностью, хим. потенциалами и др. термодинамич. параметрами, зависящими от координат и времени. Количеств. описание неравновесных процессов заключается в составлении ур-ний баланса для элементарных объёмов на основе законов сохранения массы, энергии и импульса, а также ур-ния баланса энтропии и феноменологич. ур-ний для рассматриваемых процессов, выражающих потоки массы, импульса и энергии через градиенты термодинамич. параметров. Методы Т. н. п. позволяют сформулировать для неравновесных процессов первое и второе начала термодинамики в локальной форме (в зависимости от положения элемента среды), получить из общих принципов, не рассматривая деталей взаимодействия частиц, полную систему ур-ний переноса, т. е. ур-ния гидродинамики, теплопроводности и диффузии для простых и сложных систем (с хим. реакциями между компонентами, с учётом эл.-магн. полей и др. факторов).

Законы сохранения. Для многокомпонентной системы поток массы в элемент объёма равен r_ku_k, где r_k -плотность, u_k- массовая скорость потока частиц данного вида; следовательно, з а к о н с о х р а н е н и я м а с с ы k -гo компонента имеет вид

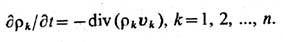
Для суммарной плотности 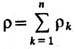закон сохранения имеет вид дr/дt= - div(ru), где u - гидродинамич., или массовая, скорость среды (ср. скорость переноса массы), зависящая от координат и времени. Для концентрации к.-л. компонента c_k=r_k/rзакон сохранения массы имеет вид 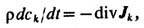где J_k= r_k(u_k -u) - диффузионный поток, d/dt = д/дt+ (ugrad) - полная, или субстанциональная, производная по времени.

Изменение импульса элементарного объёма может происходить за счёт движения частиц, внутр. напряжений в среде P_ab и внеш. сил F_k, действующих на единицу массы k -гo компонента. З а к о н с о х р а н е н и я и м п у л ь с а, применённый к элементарному объёму среды, позволяет получить осн. ур-ния гидродинамики ( Навье - Стокса уравнения):

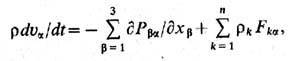
где u_a- декартовы компоненты скорости u, P_ab=pd_ab + p_ab- тензор напряжений, р -давление, d_ab- символ Кронекера, p_ab - тензор вязких напряжений. З а к о н с о х р а н е н и я э н е р г и и для элементарных объёмов представляет собой первое начало термодинамики в Т. н. п. Плотность полной энергии складывается из плотности кинетич. энергии ru²/2, плотности потенц. энергии и плотности внутр. энергии ru (энергии теплового движения частиц и энергии их короткодействующих взаимодействий). Для рм из закона сохранения энергии получается ур-ние баланса (первое начало термодинамики в Т. н. п.):

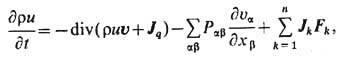
где J_q - поток тепла, 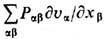-работа внутр. напряжений, 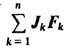- работа внеш. сил. Следовательно, внутр. энергия рм не сохраняется, сохраняется лишь полная энергия.

Уравнение баланса энтропии. Второе начало термодинамики в Т. <н. <п. выражает баланс энтропии 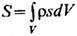(s - плотность энтропии на единицу массы) вследствие поступления потока энтропии J_s,полн из окружающей среды и возникновения её в самой системе вследствие необратимых процессов с интенсивностью источника s (локальное производство на единицу объёма в единицу времени):

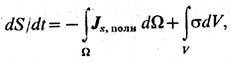
s>=0, dW - элемент поверхности системы. Отсюда следует ур-ние баланса энтропии в дифференц. форме:

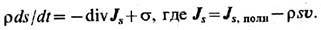
Если имеют место необратимые процессы, s > 0, энтропия (в отличие от массы, энергии и импульса) не сохраняется. В Т. н. п. принимают, что уд. энтропия s является такой же ф-цией внутр. энергии и, уд. объёма w=1/rи концентраций c_k, как и в состоянии полного термодинамич. равновесия, и, следовательно, для неё справедливы обычные термодинамич. равенства (г и п о т е з а л о к а л ь н о г о р а в н о в е с и я). Эту же гипотезу используют и в неравновесной статистич. термодинамике. Предполагают, что термодинамич, ф-ла 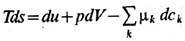остаётся справедливой и для элемента массы вдоль траектории его центра масс:

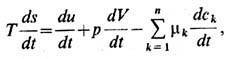
где все производные во времени являются полными.

Для плотности потока энтропии получается выражение, зависящее от плотности потока тепла J_q и плотности потока диффузии J_k:

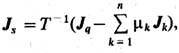
адля локального производства энтропии - выражение, зависящее от потоков и градиентов термодинамич. параметров:

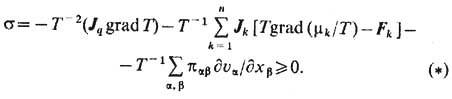
Т. <о., локальное производство энтропии вызывается необратимыми процессами теплопроводности, диффузии и вязкости. В системах с хим. реакциями появляется ещё один член, связанный с хим. сродством реакций.

Положительность локального производства энтропии (s>0), очевидная из ф-лы (*), выражает в Т. <н. <п. закон возрастания энтропии (второе начало термодинамики). Возможное изменение плотности энтропии вследствие втекания её в элемент объёма или вытекания из него не связано с необратимыми процессами и может иметь любой знак. Интегрирование ур-ния баланса энтропии по объёму системы с учётом (*) даёт для полной энтропии S соотношение 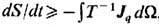, эквивалентное теореме Карно - Клаузиуса.

Локальное производство энтропии (*) представляет собой сумму произведений потоков (напр., диффуз. потока J_k, теплового потока J_q, тензора вязких напряжений p_ab) и сопряжённых им термодинамич. сил Х_i:

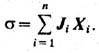
Термодинамич. силы Х_i пропорц. градиентам термодинамич. параметров, вызывающим неравновесные процессы. Величины J_i , X_i могут быть векторами (теплопроводность и диффузия), тензорами (сдвиговая вязкость), скалярами (объёмная вязкость, скорость хим. реакции). Поэтому со-ответств. процессы наз. векторными, тензорными или скалярными.

Феноменологические уравнения. В Т. н. п. исходят из того, что при малых отклонениях системы от термодинамич. равновесия возникающие потоки линейно зависят от термодинамич. сил и описываются феноменологич. ур-ниями типа 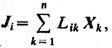L_ik - (феноменологич.) кинетические коэффициенты, или коэф. переноса (их наз. также онсаге-ровскими кинетич. коэф.). В прямых процессах термодинамич. сила X_k вызывает поток J_k, напр. градиент темп-ры вызывает поток теплоты ( теплопроводность), градиент концентрации - поток вещества ( диффузию), градиент скорости- поток импульса (к-рый определяет вязкость), электрич. поле - электрич. ток (электропроводность). Такие процессы характеризуются онсагеровскими кинетич. коэф., L_ii>0, пропорц. коэф. теплопроводности, диффузии, вязкости, электропроводности, к-рые также наз. кинетич. коэф. или коэф. переноса. Термодинамич. сила X_k может вызывать поток J_i и при i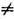k, напр. градиент темп-ры может вызывать поток вещества в многокомпонентных системах (термодиффузия, или С о р е э ф ф е к т), а градиент концентрации - поток теплоты (диффузионный термоэффект, или Дюфура эффект). Такие процессы наз. п е р ек р ё с т н ы м и или налагающимися эффектами; они характеризуются коэф, L_ik при i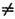k. С учётом феноменологич. ур-ний производство энтропии

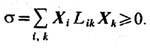
В стационарном состоянии величина s минимальна при заданных внеш. условиях, препятствующих достижению равновесия (Пригожина теорема). В состоянии термодинамич. равновесия s = 0.

Одна из осн. теорем Т. н. п.- Онсагера теорема взаимности, связанная с инвариантностью ур-ний движения относительно обращения времени, согласно к-рой в отсутствие магн. поля и вращения системы как целого онсагеров-ские кинетич. коэф. для потоков одинаковой чётности симметричны: L_ik = L_ki. Если на систему действует внеш. магн. поле Н или она вращается с угл. скоростью w, то

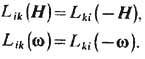
Это связано с тем, что силы Лоренца и Кориолиса не изменяются при изменении скоростей всех частиц на обратные лишь в том случае, если одновременно меняется на противоположное направление магн. поля или скорости вращения (см. Онсагера теорема).

При определ. свойствах пространственной симметрии системы феноменологич. ур-ний упрощаются. Напр., в изотропной системе потока и термодинамич. силы, имеющие разную тензорную размерность, не могут быть связаны между собой (частный случай Кюри принципа в Т. <н. п.). Поэтому в производство энтропии могут входить произведения потоков и термодинамич. сил лишь одинаковой тензорной размерности: скаляры, полярные векторы, аксиальные векторы, симметричные тензоры с нулевым следом.

С учётом принципа Кюри и соотношений Онсагера Т. н. п. даёт для потока тепла J_q и потока J₁ массы первой компоненты в бинарной ( п =2)смеси феноменологич. ур-ния

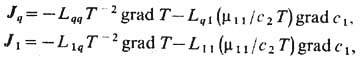
где с₁.- концентрация первой компоненты, m₁₁ =( дm₁/ дc₁)_p,T, L_1q = L_q1.

Вместо феноменологич. коэф. L_qq. L₁₁, L_1q можно ввести коэф. теплопроводности l=L_qq/T², коэф. диффузии D·=L₁₁m₁₁/rc₂T, коэф. термодиффузии D' = L_1q/rc₁c₂T², коэф. Дюфура D " = D'.

В случае вязкого течения изотропной жидкости феноменологич. ур-ние для тензора вязких напряжений имеет вид

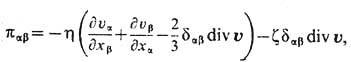
h-сдвиговая вязкость, z - объёмная вязкость, d_ab - символ Кронекера.

Т. н. п. позволяет описать неравновесные процессы в прерывных системах, напр. перенос тепла и массы между резервуарами, связанными капилляром, пористой стенкой или мембраной, если можно пренебречь объёмом капилляра или пор. В этом случае термодинамич. параметры меняются скачком. Если ввести приведённые величины:

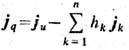
поток тепла (где j_u - изменение внутр. энергии, h_k- уд. энтальпия), потоки диффузии j_k=j_k-c_kj_n/c_n, (k=1, 2, .,., n-1), объёмный поток 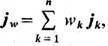то они пропорц. термодинамич. силам - конечным разностям D T/T², (D,m_m)_T,p/T, D р/Т, и феноменологич. ур-ния имеют вид:

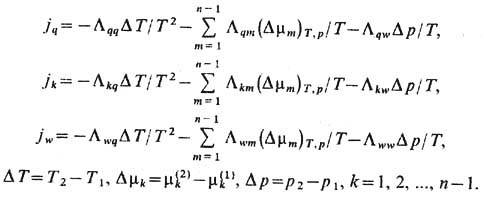
Эти ур-ния описывают эффект термомолекулярного давления- возникновение конечной величины Dp/DT при j_q = 0, j_w = 0, термоэффузию - возникновение разности концентраций Dс _k/DT при j_q=0, j_w = 0, механокалорич. эффект - существование стационарного состояния с переносом тепла при DT=0 и фиксированном перепаде давления D р (при j_k = 0). Т. <н. <п. прерывных систем позволяет описать также осмотическое давление (см. Осмос )и электрокинетические явления.

Т. н. п. используют для объяснения мн. неравновесных явлений в проводниках, напр, термоэлектрических явлений, гальваномагнитных явлений, термогальваномагнит-ных явлений. Она даёт теоретич. основу для исследования открытых систем.

Вывод законов Т. н. п. из законов механики (классич. и квантовой) и получение выражений для кинетич. коэф, через параметры, характеризующие строение вещества, входят в задачу н е р а в н о в е с н о й с т а т и с т и ч е с к о й т е р м о д и н а м и к и, к-рая относится к Т. н. <п. так же, как статистич. термодинамика к термодинамике (см., напр., Гpuнa - Кубо формулы). Обоснование Т. <н. п. для газов даёт кинетическая теория газов.

Лит.: Пригожин И., Введение в термодинамику необратимых процессов, пер, с англ., М., 1960; Термодинамика необратимых процессов, пер. с англ., М., 1962; де Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Хаазе Р., Термодинамика необратимых, процессов, пер. с нем., М., 1967; Зубарев Д. Н., Неравновесная статистическая термодинамика, М.. 1971; Дьярмати И., Неравновесная термодинамика. Теория поля и вариационные принципы, пер. с англ., М., 1974; К айзер Д., Статистическая термодинамика неравновесных процессов, пер. с англ., М., 1990. Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.