РИДБЕРГОВСКИЕ СОСТОЯНИЯ

РИДБЕРГОВСКИЕ СОСТОЯНИЯ

- состояния атомов, ионов и молекул сбольшими значениями главного квантового числа n (высоковозбуждённыесостояния). Названы в честь И. Р. Ридберга (J. R. Rydberg), впервые экспериментальноисследовавшего атомные спектры вблизи границы ионизации [1].

Р. с. атомов и ионов характеризуются чрезвычайно малыми (по атомныммасштабам) ионизац. потенциалами, большими временами жизни (т. к. вероятностьизлучат. квантовых переходов с них мала) и большими радиусами орбит высоковозбуждённого(ридберговского) электрона. Р. с. подобны состояниям атома водорода. Переходымежду соседними Р. с. лежат в радиодиапазоне. Большое значение п позволяетприменять для описания Р. с. квазиклассич. приближение и использовать дляних понятия классич. механики. Большие размеры орбит и малые энергии связиридбертовского электрона обусловливают высокую чувствительность Р. с. квоздействию электрич. и магн. полей и большие эфф. сечения взаимодействияатомов в Р. с. с заряженными частицами.

В табл. 1 приведены значения осн. характеристик атомов и атомных ионов, <находящихся в Р. с.

Табл. 1.

Систематич. изучение Р. с. стало возможным с нач. 1970-х гг. благодаряуспехам лазерной спектроскопии, позволившей исследовать в лаб. условияхР. с. с га ~300, а также радиоастрономии, т. к. в межзвёздных облаках былиобнаружены линии поглощения между Р. с. с га 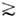700.

Волновые функции и энергии ридберговских состояний атомов. Волновыефункции Р. с. с хорошей точностью могут быть представлены как произведениеволновых ф-ций ридберговского электрона и оставшейся атомной системы -атомного остатка. Свойства атома в Р. с. в основном определяются волновойф-цией высоковозбуждённого электрона, к-рая является собств. ф-цией гамильтониана:

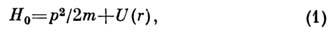
где 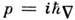- оператор импульса, U(r) - потенциальная энергия взаимодействияридберговского электрона с атомным остатком. При расстояниях r электронаот атомного ядра, много больших размеров атомного остатка, U(r )переходитв кулоновский потенциал: U(r) = Ze²/r.

Энергии Р. с. изолиров. атома, отсчитанные от границы ионизации, определяютсяф-лой Ридберга:

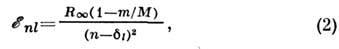
где М - масса атомного остатка,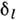- квантовый дефект, слабо зависящий от n и для орбитальногоквантового числа ll. Величины 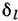для S-, Р- и D -состояний атомов щелочных металлов приведеныв табл. 2.

Табл. 2.

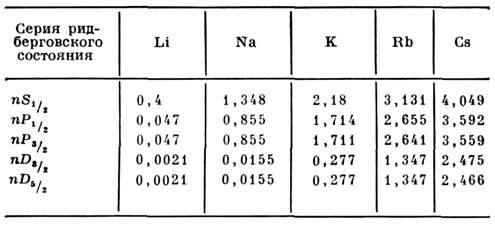
Вероятности излучат. квантовых переходов атома на Р. с. быстро падаютс ростом п и l. Для изолиров. атома в Р. с. с данными гаи l время жизни 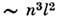. Если распределение атомов по l термодинамически равновесное [~(2l+ 1)], то вероятность 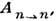излучат. переходов между Р. с. с n и n' определяется ф-лойКрамерса (с ошибкой менее 20%):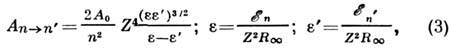

где 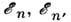- энергииуровней, отсчитанные от границы ионизации. Ср. вероятность перехода с данногоуровня на все др. уровни энергии есть величина, обратная ср. времени жизнисистемы на данном уровне.

Ридберговские состояния в электрическом поле принципиально нестационарны- происходит ионизация атома полем. Однако для слабых полей вероятностьавтоионизации ( ионизации полем )экспоненциально мала и Р. с. можносчитать квазистационарными. В электрич. поле высоковозбущдённые уровниэнергии испытывают штарковское расщепление и сдвиг (см. Штарка эффект), их волновые ф-ции являются собств. ф-циями гамильтониана:

где H₀ - гамильтониан (1) атома в отсутствие поля. <Если потенциальная энергия U(r )имеет кулоновскую природу (т. е. Н ₀ - гамильтониан водородоподобного иона), то ур-ниеШрёдингера, соответствующее гамильтониану (4), разделяется в параболич. <координатах. Проекция магн. момента на направление поля по-прежнему являетсяинтегралом движения. С точностью до второго порядка теории возмущений энергиястационарных состояний, отсчитанная от границы ионизации, даётся выражением

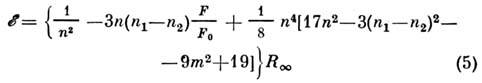
(n₁, n₂ - параболич. квантовые числа, <удовлетворяющие условию: n₁ + n₂ + 1 = n - т, т - магн. квантовое число). Выражение fe-ro порядка теории возмущенийприведено в [2]. Ф-ла (5) справедлива и для Р. с. в неводородоподобныхатомах, если масштаб штарковского расщепления, определяемый вторым слагаемым, <превышает разность энергий между состояниями с разными 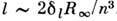. На рис. 1 в качестве примера приведена схема уровней Li в электрич. поле.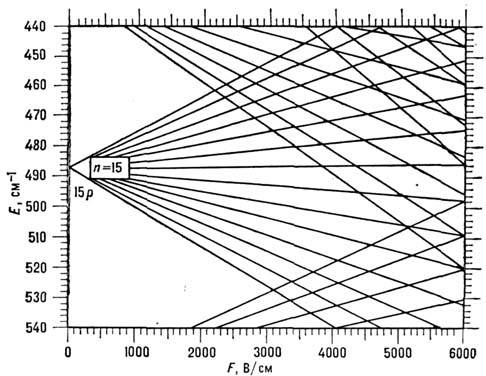

Рис. 1. Схема уровней энергии атома Li в электрическом поле для n~ 15 (|m| = 1).

Вероятность ионизации электрич. полем водородоподобных атомов в Р. с. <определяется асимптотич. ф-лой [2]:

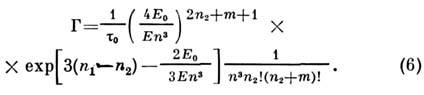
Вероятность ионизации атома в Р. с. резко возрастает, когда напряжённостьэлектрич. поля Е приближается к значению 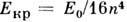, при к-ром возможна автоионизация в рамках классич. механики.

Ридберговские состояния в магнитном поле. В отличие от обычныхслабовозбуждённых состояний, для к-рых осн. роль играет парамагн. взаимодействиеатома с магн. полем (см. Зеемапа эффект, Пашена - Бака эффект), дляатомов в Р. с. важную роль играет диамагн. взаимодействие, очень быстрорастущее с увеличением п. Р. с. в магн. поле описывается гамильтонианом:

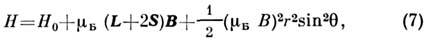
где L и S - полный момент и спин атома соответственно, В - магн. индукция,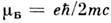- магнетон Бора,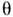- угол между радиусом-вектором ридберговcкого электрона и вектором напряжённостимагн. поля. Второе слагаемое описывает парамагнитное, третье - диамагнитноевзаимодействия. Для Р. с. диамагн. взаимодействие растёт 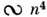и для высоких п становится определяющим. В слабых полях осн. рольиграет второе слагаемое, к-рое даёт расщепление по m-компонентам с характернойвеличиной 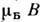,качественно такое же, как и для слабо возбуждённых состояний. С ростомнапряжённости поля увеличивается вклад диамагн. взаимодействия, к-рое связываетсостояния с одинаковыми m_l и 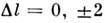.[Для состояния 4p ( т =1) в атоме водорода диамагн. и парамагн. <взаимодействия выравниваются при В =2*10⁷ Гс.] Каждыйуровень с квантовыми числами п и т расщепляется на компонент. С дальнейшим увеличением напряжённости поля начинают перемешиватьсяуровни с разными п и спектр водорода в магн. поле (рис. 2) становитсяпохожим на спектр атома в электрич. поле. В случае предельно сильных полейосн. роль играет взаимодействие с магн. полем и Р. с. являются состояниямиЛандау (см. Ландау уровни,). Кулоновское взаимодействие при этомможно рассматривать как возмущение.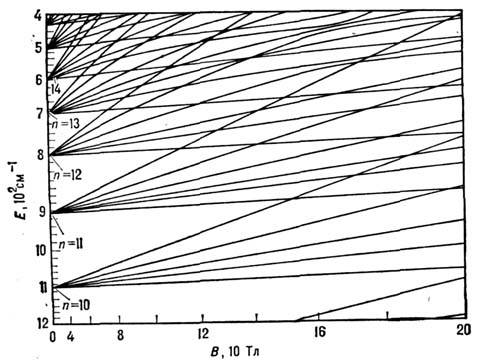

Рис. 2. Схема уровней энергии атома H в ридберговских состоянияхв магнитном поле (т = 1, чётные состояния).

Взаимодействие атомов в ридберговском состоянии с заряженными частицами. Эфф. сечения s квантовых переходов в атомах, находящихся в Р. с. пристолкновениях с заряженными частицами (электронами, ионами), растут какгеом. сечение ~n⁴. Для переходов с малыми 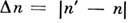осн. роль играет дальнодействующее дипольное взаимодействие, к-рое приводитк 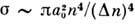,а при больших энергиях внеш. частицы 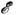зависимость от энергии даётся множителем 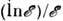(квантовый логарифм!). С ростом 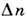всё большую роль начинает играть короткодействующее взаимодействие, позволяющеепренебречь полем атомного остатка в процессе столкновения, а само столкновениерассматривать в рамках классич. механики. Этот подход, называемый классич. <бинарным приближением, позволяет получить 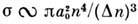;при больших энергиях 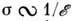.В приближении Борна сечение перехода 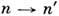при столкновении с электронами определяется ф-лой (3):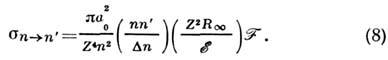

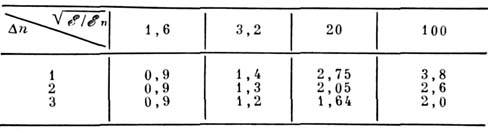
Ф-ция 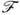для п =100 приводится в табл. 3.

Т а б л. 3.

Переходы между Р. с. при столкновениях с электронами являются осн. причинойдополнительного (помимо доплеровского) неупругого уширения рекомбинационныхрадиолиний, наблюдаемых от ряда астрофиз. объектов (планетарных туманностей, <межзвёздной среды, зон НИ и т. д.).

В столкновит. переходах между Р. с. с одинаковым п осн. роль, <как правило, играют ионы. Наиб. велики сечения для переходов между соседнимиуровнями 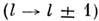, обусловленные дипольным взаимодействием. Они на порядок и более превосходятгеом. сечение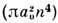

Взаимодействие атомов в ридберговском состоянии с нейтральными атомами. Если п достаточно велико, то сечение процесса взаимодействияатомов в Р. с. с нейтральными атомами выражается через амплитуду рассеяниясвободного электрона на нейтральном атоме и амплитуду рассеяния атома наположительно заряженном атомном остатке. Напр., в результате взаимодействияс нейтральными атомами Р. с. испытывают уширение 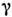и сдвиг 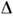,пропорциональные концентрации возмущающих частиц N: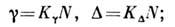

коэф.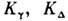выражаются через амплитуду упругого рассеяния электрона на атоме и параметрывзаимодействия нейтрального атома с атомным остатком [3] и для достаточнобольших п стремятся к константам; в промежуточной области их поведениеможет быть весьма сложным и зависит от конкретного вида возмущающих частиц. <Для атомов Cs в Р. с., возмущаемых, напр., атомами Аг, асимптотич. значения 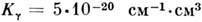,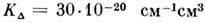; есливозмущающими атомами являются атомы Cs, то 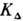увеличивается в 20 раз, а 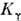- на 2 порядка. Асимитотич. значений коэф.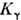и 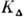достигаютпри взаимодействии с атомами инертных газов при 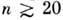, а при взаимодействии с атомами щелочных металлов при 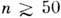. Поведение сечений др. процессов взаимодействия атомов в Р. с. с нейтральнымиатомами (перемешивание состояний по l, дезориентация и др.) качественноаналогично поведению сечений уширения.

Лабораторные эксперименты. Р. с. в лаб. условиях создаются чаще всеговозбуждением атома из осн. состояния одним или неск. световыми пучкамибольшой интенсивности (по крайней мере на первом этапе возбуждения - накачке).Для накачки обычно используется N₂ -лазер или вторая (третья)гармоника лазера на неодимовом стекле. Чтобы получать Р. с. с заданнымиквантовыми числами п, l, т, на втором этапе атомную систему возбуждаютизлучением мощных перестраиваемых лазеров на красителях.

Для регистрации Р. с. наиб. распространение получили флуоресцентныйметод и метод ионизации электрич. полем. Флуоресцентный метод основан наанализе каскадного испускания света при переходах атома из Р. с. Этот методобладает селективностью, однако интенсивность регистрируемого излученияв видимой области в этом случае мала. Флуоресцентный метод используют, <как правило, для исследования Р. с. с п <20.

В методе ионизации электрич. полем регистрируются электроны, освобождающиесяв результате ионизации атома в Р. с. при воздействии на него электрич. <поля. В этом случае селективность обеспечивается чрезвычайно резкой зависимостьювероятности ионизации от квантовых чисел п и т. Чаще всегоэтот метод используется в режиме с временным разрешением: после импульсноговозбуждения Р. с. подаётся пилообразный импульс электрич. поля. КаждоеР. с. в разрешённом по времени ионизац. сигнале даёт пик через строго определённоевремя от момента включения поля. Метод отличается простотой, высокой чувствительностьюи в отличие от флуоресцентного метода особенно эффективен при исследованииР. с. с большими п, когда для ионизации не требуется высоких напряженийэлектрич. полей.

Спектры атомов и ионов в Р. с. исследуются разл. методами. С помощьюобычных многомодовых лазеров достигается спектральное разрешение порядкадоплеровской ширины уровня, что позволяет исследовать Р. с. с 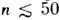. Если требуется более высокое разрешение, то используют метод скрещенныхатомно-лазерных пучков, дающий разрешение в несколько Мгц, или методы нелинейнойлазерной спектроскопии. Напр., методом двухфотонной спектроскопии был полученспектр с разрешением порядка Кгц. В тех случаях, когда интерес представляютинтервалы между соседними Р. с., более удобны методы радиоспектроскопии,, квантовых биений и пересечения уровней (см. Интерференция состояний)[2]. Вместо настройки частоты излучения на частоту перехода между Р. <с., на заданную внеш. полем частоту можно настраивать сами Р. с. В этомслучае Р. с. позволяют усиливать слабый микроволновый сигнал. Этим методомполучена чувствительность 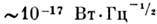в миллиметровом диапазоне; есть основания ожидать повышение чувствительностиещё на 2 порядка.

Особый интерес представляют эксперименты с атомами в Р. с. в резонаторах. <Для п ~30 переходы между Р.. с. лежат в миллиметровом диапазоне, <для к-рого существуют резонаторы с очень высокой добротностью. В то жевремя влияние электрич. поля на атомы в Р. с. более значительно, чем, напр.,для молекулярных вращат. уровней энергии, поэтому с помощью Р. с. впервыеудалось продемонстрировать ряд эффектов квантовой электродинамики, предсказанныхв 50- 60-е гг.: подавление спонтанного радиац. перекода в резонаторе, нутациюРаби - взаимодействие с полек одного фотона в резонаторе, кооперативныеэффекты Дикке для неск. атомов (см. Сверхизлучение )и др. [4].

Астрофизические приложения ридберговских состояний. Первые наблюденияизлучат, переходов между Р. с. от астрофиз. объектов (лини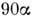и и 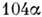) быливыполнены в СССР [5]. Радиолинии излучения, соответствующие переходам междуР. с., наблюдаются вплоть до п ~300 от галактич. зон Н II, планетарныхтуманностей, центральных областей нашей Галактики и нек-рых др. галактик. <Обнаружены также линии Не, Не II, С II. Осн. механизмом образования Р. <с. в астрофиз. объектах является фоторекомбинация, поэтому радиолинии излученияназ. также рекомбинац. радиолиниями. Радиолинии между Р. с. играют важнуюроль в диагностике астрофиз. объектов. Для п< 100 ширина такихлиний обусловлена эффектом Доплера и позволяет судить о ионной темп-рекосмич. плазмы. Для более высоких п в уширение вносят вклад столкновенияс электронами, и т. о. по ширине радиолиний можно оценить также плотностьэлектронов. Отношение интенсивностей радиолиний и континуума даёт электроннуютемп-ру.

В межзвёздных облаках обнаружены радиолинии поглощения, принадлежащиеиону С II и соответствующие переходам между Р. с. с п

Лит.:1) R у d b е r g J. R., «Z. Phys. Chem.», 1890, Bd 5, S.227; 2) Ридберговские состояния атомов и молекул, пер. с англ., М., 1985;3) Вайнштейн Л. А., Собельман И. И., Ю к о в Е. А., Возбуждение атомови уширение спектральных линий, М., 1979; 4) Нагое he S., Raimond J. M.,«Adv. in Atom. and Molec. Phys.», 1985, v. 20, p. 347; 5) Сороченко Р. <Л., Рекомбинациошше радиолинии, в кн.: Физика космоса, 2 изд., М., 1986. И. Л. Бейгман,

Ридберговские состояния молекул. Высоковозбуждённые электронныесостояния М., так же как и атомные, подобны серии состояний атома водорода. <Ридберговские орбитали молекул обозначаются главным п и орбитальным l квантовыми числами и типом симметрии группы симметрии молекулы (напр., nsa₁, npb₁). Энергия Р. с. (отсчитываемаяот границы ионизации молекул) определяется ф-лой Ридберга (2). Для молекулы, <состоящей из атомов первого периода, величина квантового дефекта 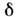для nd -орбиталей очень мала (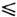0,1),для nр -орбиталей несколько выше (0,3-0,5), а для ns- орбиталейзначительно больше (0,9-1,2). Стабильность Р. с. молекул зависит от стабильностиосн. состояния или низколежащего возбуждённого состояния молекулярногоиона, получающегося при удалении ридберговского электрона, т. к. ридберговскаяорбиталь, вообще говоря, является несвязывающей. Стабильность иона зависитот того, удаляется ли электрон со связывающей, разрыхляющей или несвязывающеймолекулярной орбитали осн. состояния нейтральной молекулы. Напр., для Н ₂ Оиз занятых молекулярных орбиталей в оси. состоянии самой верхней являетсянесвязывающая молекулярная орбиталь 1b₁. Поэтому осн. <состояние иона Н ₂ О ⁺, получающегося при удалении электронас этой орбитали, столь же стабильно, как и осн. состояние молекулы Н ₂ О:практически все Р. с. молекулы Н ₂ О, сходящиеся к осн. состояниюиона Н ₂O⁺, стабильны.

Если электрон переходит с низколежащей на более высокую молекулярнуюорбиталь с тем же п, то получающиеся состояния наз. субридберговскими. Т. к. п не является вполне определённым квантовым числом длянизких молекулярных орбиталей, субридберговские состояния мало отличаютсяот Р. с. молекул, хотя субридберговские орбитали могут быть и связывающими.

Р. с. молекул отличаются от Р. с. атомов гл. обр. благодаря колебаниям, <вращениям и возможности диссоциации ионного остова молекулы. Если ионныйостов находится в возбуждённом колебат. состоянии, то ридберговский электронпри проникновении в ионный остов (что происходит довольно редко, с вероятностью 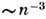) может испытать неупругое столкновение с остовом, приобрести достаточнуюкинетич. энергию за счёт колебат. энергии остова и привести к ионизациимолекулы, наз. колебательной автоионизацией. Процесс автоионизации возможентакже за счёт вращения. Высоковозбуждённые Р. с. молекул обычно лежат такблизко, что энергетич. интервал между ними бывает такого же порядка илидаже меньше, чем квант колебат. или вращат. энергии молекулы. Поэтому часторазделение электронного и ядерного движений, принятое в приближении Берна- Оппенгеймера, для молекул в Р. с. становится непригодным.

Лит.: Герцберг Г., Электронные спектры и строение многоатомныхмолекул, пер. с англ., М., 1969; Ридберговские состояния атомов и молекул, <под ред. Р. Стеббингса, Ф. Данвинга, пер. с англ., М., 1985. М. Р. Алиев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.