ПРОСТРАНСТВЕННАЯ КОГЕРЕНТНОСТЬ

ПРОСТРАНСТВЕННАЯ КОГЕРЕНТНОСТЬ

волнового поля - одна из его характеристик, определяющая статистич. связь, корреляцию между параметрами поля в разных точках пространства.

П. к. лазерного пучка определяет статистич. связь между значениями поля не в произвольных точках пространства, а в разных точках поперечного сечения пучка. Вдоль направления распространения лазерного пучка статистич. связь определяется временной когерентностью излучения. Спонтанные шумы, возбуждение многих поперечных мод приводят к тому, что поперечная пространственная структура лазерных пучков становится случайной, а их поле излучения оказывается не полностью когерентным в пространстве. Вместе с тем масштаб поперечных корреляций лазерного излучения (поперечный радиус когерентности, радиус корреляции) значительно превосходит соответствующий масштаб нелазерных источников излучения. По величине отношения значений радиуса корреляции к радиусу пучка лазерного излучения различают два предельных случая излучения: многомодового по поперечным индексам и одномодо-вого.

Многомодовые лазерные пучки. В случае возбуждения большого числа N поперечных мод со статистически независимыми фазами пространственная статистика лазерных пучков близка к гауссовой. При этом поперечная пространственная корреляц. ф-ция, ф-ция взаимной когерентности, определяемая выражением

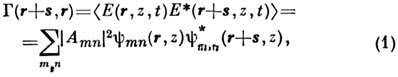
похожа на корреляц. ф-цию -коррелированного излучения, дифрагированного на круглом отверстии. В выражении (1) E(r,z,t)- комплексная напряжённость элек-трич. поля, действительная часть - ReE(r,z,t), A_mn- амплитуда моды с поперечными индексами т и п, - модовая ф-ция, описывает распределение интенсивности моды в поперечном сечении. Направление оси z совпадает с направлением распространения лазерного пучка, двумерный вектор лежит в плоскости, перпендикулярной оси z. На рис. 1

Рис. 1. Модуль степени пространственной когерентности излучения твердотельного лазера для N поперечных мод: 1 - для N= 830; 2 - для N= 10⁴.

изображена нормированная корреляц. ф-ция (1), т. е. степень П. к.

для случая = 0 и разл. числа поперечных мод. Значение радиуса корреляции, определённого, напр., по уровню 0,5 от макс. значения |g(s,0)|, равного единице, существенно зависит от геометрии резонатора и числа поперечных мод N. Так, для многомодовых лазерных пучков, возбуждаемых в резонаторе с плоскими прямоугольными зеркалами, радиус корреляции d/N, где 2d- размер зеркала вдоль измеряемого направления. В случае сферич. резонатора с круглыми зеркалами где а(z) - радиус низшей моды на расстоянии z от перетяжки пучка. Последняя зависимость радиуса корреляции получила эксперим. подтверждение. Кроме того, значение радиуса корреляции r _кс увеличивается к краю лазерного пучка, т. е. много-модовые лазерные пучки, возбуждаемые в сферич. резонаторах, являются статистически неоднородными. Для числа мод N =10⁴ отношение поэтому, если радиус пучка составляет 1-10 мм, радиус корреляции оказывается равным 10-100 мкм. При наличии неоднородностей в активной лазерной среде даже для плоского резонатора более адекватной оказывается модель сферич. резонатора.

Одномодовые лазерные пучки; предельная П. к. и стохастическое блуждание пучка. При генерации лишь осн. поперечной моды ТЕМ ₀₀ (индексы m=n=0) усиление в лазере достаточно для компенсации потерь, состоящих из потерь в среде, на излучение и дифракционных. Однако этого усиления недостаточно для компенсации потерь на высших модах, поскольку с увеличением номера поперечного индекса m и (или) n дифракц. потери растут. Спонтанное излучение усиливающей среды не только является затравкой для возбуждения осн. моды, но и поддерживает на определённом уровне интенсивность подпороговых высших мод. Вследствие излучения последних П. к. одномодовых лазерных пучков не является полной. Но в пределах ширины пучка степень П. к., напр. для излучения гелиево-неоновых лазеров, отличается от 1 не более чем на 10^-4 - 10^-6 (рис. 2).

Рис. 2. Зависимость 1 - |g(s,0)| в одночастотном режиме генерации лазера ЛГ-159 (l = 633 нм): точки - экспериментальные данные, кривая - теоретическая.

Осн. влияние на предельную степень П. к. моды ТЕМ ₀₀ оказывают ближайшие подпороговые высшие моды, т. е. моды с поперечными индексами m = 0, n=1 и m = 1, n = 0. Для мод сферич. резонатора

и значений r{0,0}, s{s,0} степень П. к.

где

Величина представляет собой отношение макс. интенсивностей подпороговой моды и осн. моды:

Здесь и u - коэф. усиления и групповая скорость на частоте осн. моды, - Планка постоянная, q _тп - дифракц. потери на соответствующей моде, R- коэф. отражения по амплитуде выходного зеркала; N₁> N₂- населённости нижнего и верхнего уровней усиливающей среды,- параметр вырождения уровня, P- мощность излучения через выходное зеркало. Из (3) видно, что значение обратно пропорц. разности дифракц. потерь излучаемой мощности Р, разности населённостей рабочих уровней.

Др. интерпретация следствия подпорогового возбуждения высших мод (т. е. не полной П. к.) - стохастич. блуждание центра осн. моды. Дисперсия этого блуждания

При радиусе пучка а₀= 0,3 мм значение = 0,5 мкм (рис. 2). С ростом мощности излучения величина s уменьшается как и может быть 10 нм.

С неполной П. к. можно также связать естеств. угл. расходимость , обусловленную спонтанным излучением лазера: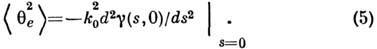

При этом дисперсия случайного блуждания

Соотношения (5), (6) дают общую связь между неполной П. к., стохастич. блужданием и естеств. угл. расходимостью лазерного пучка. Выражения (4), (6) в совокупности с (3) можно рассматривать как некий пространственный аналог ф-лы Шавлова - Таунса для естеств. ширины линии одночастотного лазерного излучения.

Неполная П. к. одномодового лазерного пучка (или естеств. угл. расходимость, или стохастич. блуждание), обусловленная принципиально не устранимыми флук-туациями - спонтанным излучением лазера, влияет, очевидно, на разрешающую способность и информативность систем оптич. записи и считывания информации.

Лит.: Ахманов С. А., Дьяков Ю., Е., Чиркин А. С., Введение в статистическую радиофизику и оптику, М., 1981; Ахманов С. А., Чиркин А, С., Белин-ский А. В., Предельная пространственная когерентность лазерного излучения, "УФН", 1993, т, 163, № 3.

А. С. Чиркин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.