ПАРАМЕТР ПОРЯДКА

ПАРАМЕТР ПОРЯДКА

- термодинамич. <величина, характеризующая дальний порядок в среде, возникающий в результате спонтанного нарушения симметрии при фазовом переходе. РавновесныйП. п. равен нулю в неупорядоченной фазе и отличен от нуля в упорядоченной. <При фазовом переходе 2-го рода П. п. непрерывно возрастает от нулевогозначения в точке перехода, а при переходе 1-го рода сразу принимает конечноезначение. Если переход происходит из неупо-рядоч. состояния с группой симметрии G в упорядоченное состояние с пониженной группой симметрии Н 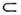G,то П. п. в равновесии инвариантен относительно преобразований из группы Н, но преобразуется по представлению группы G, отличномуот единичного. Вблизи точки фазового перехода 2-го рода Т _с, гдеП. п. мал, он преобразуется по одному из неприводимых представлений группы G; вклад остальных представлений, согласно Ландау теории, мално параметру 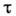=1 - - Т/ Т _с.
Примеры П. п.: 1). Отклонение зависящейот координат плотности атомов в кристалле от её ср. значения преобразуетсяпод действием общей группы трансляций и пространственных вращений, входящихв группу симметрии G изотропной жидкости, но остаётся инвариантнымотносительно преобразований из пространственной группы симметрии кристалла.2). Анизотропная часть тензора дпэлектрич. проницаемости в жидком кристалле преобразуется под действием группы пространственных вращений как симметричныйтензор с нулевым следом. 3). Намагниченность в ферромагнетике преобразуетсякак вектор при вращениях подсистемы спинов и меняет знак при обращениивремени. 4). Волновая ф-ция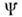 бозе-конденсата в сверхтекучем ⁴ Не (см. Гелий жидкий, Сверхтекучесть )преобразуетсяпод действием калибровочного преобразования группы U(1), входящейв группу G изотропной жидкости: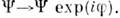5). Комплексная матрица 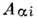в сверхтекучем ³ Не преобразуется как вектор по второму индексупри пространственных вращениях, как вектор по первому индексу при спиновыхвращениях, умножается на 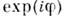при калибровочных преобразованиях, переходит в комплексно сопряжённую матрицупри обращении времени и меняет знак при пространственной инверсии. Согласнотеории Ландау, равновесное значение П. п. вблизи фазового перехода 2-города находят, минимизируя функционал Гинзбурга - Ландау, инвариантный относительнопреобразований из группы G.
Вырождение в упорядоченных фазах. Поддействием преобразований из группы G, не входящих в подгруппу Н,П. п., а вместе с ним и состояние системы изменяется без изменения энергии. <Т. о., в упорядоченной фазе имеется вырожденце равновесных состояний. Совокупность R всех таких равновесных состояний образует фактор-пространство R= G/H. В случае ферромагнетика R является сферой радиуса М, на к-рой принимает свои значения равновесная намагниченность М. В сверхтекучем ⁴ Не область R является окружностью, <соответствующей значениям фазы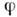 волновой ф-ции 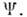Жёсткость упорядоченного состояния приводит к появлению коллективных возбуждений- колебаний П. п. вблизи любого из его равновесных значений. Особенно выделяютсят. п. голостоуновские моды, частота к-рых обращается в нуль в пределебесконечной длины волны. При этих колебаниях П. п. не выходит за рамкипространства R. Число голдстоуновских мод обычно совпадает с размерностьюпространства R. Напр., второй звук в сверхтекучем ⁴ Не- колебания фазы 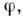спиновыеволны в ферромагнетике - колебания направления намагниченности.

Неоднородные состояния П. п. Непрерывноевырождение равновесных состояний упорядоченных фаз приводит к появлениюсостояний, в к-рых П. п. зависит от координат. Такие неоднородные состоянияможно создавать при помощи внеш. полей, они могут существовать и в видеметастабильных дефектов структуры, таких, как квантованные вихри всверхтекучем ⁴ Не, дислокации, в кристаллах, доменныестенки в ферромагнетиках, дисклинации в жидких кристаллах,солитоны всверхтекучем ³ Не, вихри Абрикосова в сверхпроводниках и др. Их устойчивость связана с топологией пространства R иобеспечивается наличием сохраняющихся топологич. инвариантов, или топологич. <зарядов (т. н. топологич. устойчивость). Напр., топологич. заряд квантованноговихря в ⁴ Не равен числу обходов фазой 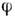окружности R при обходе вокруг вихря; это совпадает с числом квантовциркуляции сверхтекучей скорости вокруг вихря. Сложение топологич. зарядовподчиняется групповому закону. Напр., в сверхтекучем ⁴ Не прислиянии двух одинаковых вихрей с топологпч. зарядами 1 возникает вихрьс топологич. зарядом 2; в сверхтекучем ³ Не при слиянии двуходинаковых вихрей может возникнуть состояние с топологич. зарядом 0.

Лит.: Ландау Л. Д., Лифшнц Е. М.,Статиотическая физика, ч. 1, 3 изд., М., 1976; Паташинский А. 3., ПокровскийВ. Л., Флуктуационная теория фазовых пореходов, 2 изд., М., 1982; ВоловикГ. Е., Минес в В. П., Физика и топология, М., 1980.

Г. Е. Воловик.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.