ПРИБЛИЖЕНИЕ

ПРИБЛИЖЕНИЕ

- приближённый метод решения дифференц. ур-ний, содержащих случайные параметры; основан на малости отношения времени корреляции воздействий 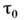ко времени корреляции отклика 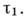Формально соответствует пределу 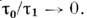Непосредственно применим лишь к причинным задачам, в к-рых значения динамич. переменных в нек-рый момент времени функционально не зависят от последующих по времени значений случайных параметров. В физ. задачах M. п. п. является гл. членом разложения по малому параметру 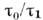и, в отличие от методов теории возмущений, допускает описание сильных флуктуации, возникающих в физ. системе под влиянием случайных воздействий.

Пусть поведение динамической системы описывается обыкновенными дифференц. ур-ниями:

Здесь 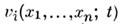- детерминиров. ф-ции своих аргументов, а - случайная ф-ция (n+1)

переменной, обладающая след, свойствами ((...) означает статистич. усреднение,

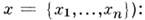
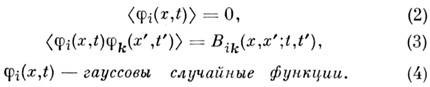
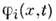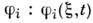В ур-нии (1) случайна как сама ф-ция при детерминиров. аргументах, так и ф-ции входящие в аргумент . Условия (2) - (4) накладываются на случайные f-ции 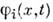при детерминиров. аргументах.

Если реальную корреляц. ф-цию (3) заменить ф-цией вида

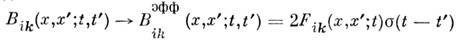
и считать, что входящие в (1) гауссовы случайные ф-ции характеризуются корреляц. ф-цией 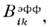то это соответствует замене истинного времени корреляции 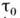нулём и эквивалентно переходу к M. п. п. При этом в (1) возникают два стремящихся к нулю временных масштаба: один - при вычислении производной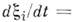

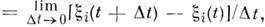другой - при стремлении к нулю 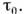Ниже предельный переход 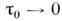совершают после выполнения перехода 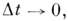т. е. предполагают, что 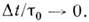Ф-ции 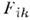находят из условия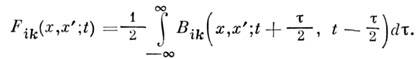

При сделанных предположениях плотность вероятностей

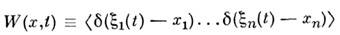
решения системы (1) удовлетворяет Эйнштейна - Фоккера- Планка уравнению

где

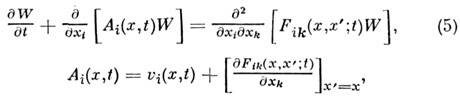
по повторяющимся индексам производится суммирование. Совместная плотность вероятностей для величин при 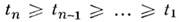в этом случае

распадается на произведение

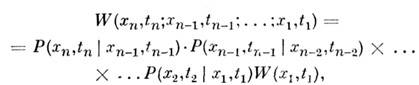
а ф-ция 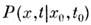(переходная вероятность) удовлетворяет по переменным х, t ур-нию (5) с нач. условием 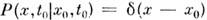T. о., случайный процесс является марковским.

В реальных физ. задачах время корреляции флуктуации всегда конечно и вопрос о пригодности M. п. п. сводится к учёту конечности малого параметра 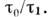Одно из условий применимости M. п. п. всегда имеет вид 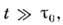но обычно возникают и др. условия.

M. п. п. применимо и к причинным задачам, описываемым ур-ниями с частными производными, однако здесь уже нет такой универсальной формулировки, как для обыкновенных дифференц. ур-ний.

Задачи, описываемые дифференц. ур-ниями с двухточечными граничными условиями (напр., в задаче о распространении волны одно из граничных условий ставится в точке возбуждения волны, а второе описывает её отражение от нагрузки в конце), непосредственно нельзя описывать M. п. п. Однако в ряде случаев такие задачи можно свести к вспомогат. задачам Коши (методом инвариантного погружения или др. способами), после чего к ним применимо M. п. п.

Лит.: Кляцкин В. И., Татарский В. И., Приближение диффузионного случайного процесса в некоторых нестационарных статистических задачах физики, "УФН", 1973, т. НО, с. 499; Введение в статистическую радиофизику, ч. I - Pытов С. M., Случайные процессы, ч. 2 - Pытов С. M., Кравцов Ю. А., Татарский В. И., Случайные поля, M., 1976-78; Кляцкин В. И., Стохастические уравнения и волны в случайно неоднородных средах, M., 1980.

В. И. Татарский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.