МАГНИТНЫЙ МОНОПОЛБ

МАГНИТНЫЙ МОНОПОЛБ

- гипотетич. частица, обладающая положит. или отрицат. "магн. зарядом" - точечным источником радиального магн. поля. М. м. можно представлять как отдельно взятый полюс длинного и тонкого пост. магнита. Магн. заряд определяет напряжённость магн. поля совершенно так же, как электрич. заряд определяет напряжённость электрич. поля.

С созданием физики как науки, основанной на опыте, утвердилось мнение, что электрич. и магн. свойства тел существенно различаются. Это мнение было чётко выражено У. Гильбертом (W. Gilbert, 1600). Установленное Ш. Кулоном (Ch. Coulomb) тождество законов притяжения и отталкивания для электрич. зарядов и магн. зарядов - полюсов магнитов (см. Кулона закон )вновь подняло вопрос о сходстве электрич. и магн. сил, однако к кон. 18 в. (в первую очередь благодаря опытам Кулона) было выяснено, что в лаб. условиях невозможно создать тело с ненулевым полным магн. зарядом. Понятие о "магнитно заряженной субстанции" было надолго изгнано из физики после работы А. Ампера (A. Ampere, 1820), в к-рой было доказано, что контур с электрич. током создаёт такое же магн. поле, как магн. диполь. Открытие Дж. К. Максвеллом (]. С. Maxwell) ур-ний для эл.-магн. поля (см. Максвелла уравнения), в особенности введение тока смещения, выявило симметрию относительно замены 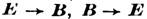(E, В - векторы напряжённости электрич. поля и магн. индукции). [В действительности, это частный случай более общей "дуальной симметрии", 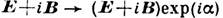при произвольном 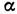.] Эта симметрия, однако, нарушается в присутствии матер. тел, т. к. свободных магн. зарядов в природе не обнаружено.

Классич. электродинамика не противоречит возможности существования магн. зарядов. Однако, в отличие от поля электрич. зарядов и токов, поле, создаваемое магн. зарядами, не может быть описано с помощью вектор-потенциала 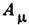(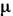=0, 1, 2, 3) непрерывного во всём пространстве. Поэтому при наличии магн. зарядов ур-ния движения заряж. частиц не выводятся из вариационного наименьшего действия принципа. В классич. электродинамике это не приводит к принципиальным трудностям (хотя и делает теорию несколько менее красивой), но квантовую динамику невозможно сформулировать вне рамок га-милътонова формализма или лагранжева формализма, основанных на вариац. принципе.

П. А. М. Дирак (Р. А. М. Dirac, 1931) создал квантовую теорию взаимодействия электрич. заряда е с магн. зарядом g, к-рая применима при условии: 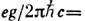=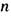, где п - целое число. Т. о., магн. заряд частицы должен быть кратен элементарному магн. заряду 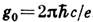, где е - элементарный электрич. заряд. Примечательно обратное утверждение: существование магн. заряда не противоречит стандартной квантовой механике только в том случае, если электрич. заряды всех частиц квантуются. (Т. о., существование М. м. объяснило бы наблюдаемую на опыте кратность электрич. зарядов частиц величине е. )Условие квантования Дирака обобщается на взаимодействие двух частиц, каждая пз к-рых обладает как электрич., так и магн. зарядом (т. н. дионов): 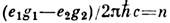. (В используемой системе единиц е и g имеют одинаковую размерность, причём заряд е фиксирован соотношением 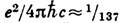.) В нерелятивистском приближении сила, действующая на дион 1 с координатами r и скоростью v со стороны диона 2, закреплённого в начале координат, равна:

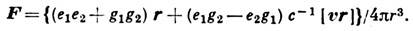
Отметим, что входящие в эту ф-лу комбинации зарядов инвариантны относительно дуального преобразования.

Условие квантования Дирака выводится из след. соображений. Поле, создаваемое М. м., может быть описано вектор-потенциалом 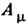, если допустить существование скачка 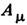на нек-рой (произвольной) поверхности S, проходящей через М. м. и делящей пространство на две связные части [By (By Цзяньсюн) и Янг (Ян Чжэньнин), 1976]. При этом напряжённость поля непрерывна на поверхности S всюду, кроме точки расположения М. м., а сама поверхность может быть произвольным образом деформирована с помощью калибровочных преобразований. Циркуляция скачка 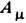по любому контуру, лежащему на S и охватывающему М. м., равна магн. потоку, исходящему из М. м., т. е. (согласно теореме Гаусса) заряду g. Контурный интеграл от 4-вектора 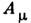даёт вклад в фазу 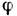волновой ф-ции электрически заряж. частицы, и скачок 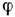, соответствующий скачку 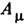на поверхности S, равен 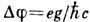. При выполнении условия Дирака 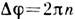, так что волновая ф-ция непрерывна во всём пространстве. К тому же скачок 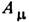не даёт вклада в напряжённость магн. поля, к-рая определяется законом Кулона, поэтому поверхность S ненаблюдаема. В качестве этой поверхности можно выбрать уходящий на бесконечность конус, в вершине к-рого находится М. м., а угол при вершине сколь угодно мал ("струна", или "нить", Дирака).

Можно показать, что эффект М. м. сводится к замене l(l+1)на 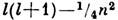( п - целое число в условии Дирака) в центробежном потенциале радиального ур-ния Шрёдингера (И. Е. Тамм, 1931), при этом орбит. угловой момент l может принимать значения 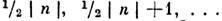. Заметим, что при нечётном п система из двух бесспиновых частиц благодаря ненулевой дивергенции магн. поля обладает полуцелым угловым моментом. Т. о., из двух бозонов с ненулевыми полными злектрич. и магн. зарядами образуется дион, подчиняющийся статистике Ферми - Дирака. Аналогично связанное состояние бозона и фермиона может быть бозонем.

В 1974 А. М. Поляков и Г.' т Хоофт (G.' t Hooft) обнаружили, что существование М. м. не только возможно, но и обязательно в полевых теориях определённого класса. В моделях великого объединения, рассматривающих симметрию относительно фазовых преобразований волновых ф-ций заряж. частиц как составную часть более широкой неабелевой калибровочной симметрии (см. Калибровочная инвариантность), эл.-магн. поле связано с мультиплетом заряж. калибровочных полей X с массами M_X~10¹⁴ ГэВ/с ² (эти массы возникают при спонтанном нарушении симметрии). Для нек-рых калибровочных групп симметрии существуют устойчивые конфигурации полей X, локализованные в области размером 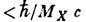и создающие вне этой области сферически симметричное магн. поле. Существование таких конфигураций зависит от топологич. свойств калибровочной группы, точнее, от того, каким образом в неё вложена подгруппа симметрии, сохранившейся после спонтанного нарушения. Стабильность этих М. м. определяется особым поведением полей на больших расстояниях от центра. Масса М. м. M_M может быть вычислена, она зависит от конкретной полевой модели, однако во всяком случае должна быть большой, M _м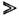M_X (по оценке, для широкого класса моделей M _м~10¹⁶ ГэВ/с ²~10^-8 г). Эти М. м. могли бы рождаться в горячей Вселенной вскоре после Большого Взрыва при фазовом переходе, связанном со спонтанным нарушением симметрии и возникновением отличных от нуля однородных скалярных полей в вакууме. Кол-во рождающихся М. м. определяется процессом развития Вселенной на ранней стадии, поэтому по их отсутствию в наст. время можно судить об этом процессе. Одно из объяснений того, что реликтовые М. м. не обнаружены, даётся теорией раздувающейся Вселенной. М. м. Полякова - т Хоофта обладают нек-рыми необычными свойствами, благодаря к-рым их было бы легко обнаружить. В частности, взаимодействие с М. м. может стимулировать распад нуклона, предсказываемый нек-рыми моделями великого объединения [А. Рубаков, 1981, К. Каллан (С. Callan), 1982], т. е. выступать в качестве катализатора такого распада.

Неоднократные попытки эксперим. обнаружения М. м. не увенчались успехом. Особенно интенсивно поиски М. м. космич. происхождения проводились с нач. 80-х гг. Эксперименты можно разделить на две группы. 1) М. м. можно обнаружить непосредственно по связанному с ним магн. потоку. Прохождение магн. заряда ng₀ сквозь сверхпроводящий контур изменит поток на 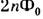" , где 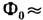2*10^-3 Гс*м ² -квант магн. потока, и явление эл.-магн. индукции приведёт к скачку тока в контуре, к-рый может быть измерен с помощью сверхпроводяшего квантового интерферометра (сквида). 2) Тяжёлый М. м. должен обладать высокой проникающей способностью и создавать на своём пути сильную ионизацию. Поэтому для поисков М. м. использовались подземные детекторы, сооружённые для изучения потоков космич. нейтрино и поисков распада протона. Проводились также поиски М. м., захваченных в магн. рудах земного и внеземного (метеориты, Луна) происхождения, а также треков, оставленных ими в слюде, заключённой в древних земных породах. Ставились и опыты с целью обнаружения процессов рождения М. м. при столкновениях частиц высокой энергии на ускорителях, однако массы таких М. м., естественно, ограничены энергией, доступной на совр. ускорителях. Наиб. сильное ограничение на возможное число М. м. в космич. пространстве дают соображения, связанные с наличием галактич. магн. полей, т. к. монополи ускорялись бы в этих полях, отбирая тем самым энергию у их источников, что приводило бы к ослаблению полей со временем. Числ. оценка этого ограничения зависит от ряда предположений, но едва ли поток космического М. м. в единичном телесном угле может превосходить 10^-12 м ^-2* стр ^-1.

Лит.: Монополь Дирака. Сб. ст., пер. с англ., М., 1970; Стражев В. И., Томильчик Л. М., Электродинамика с магнитным зарядом. Минск, 1975; Коулмен С., Магнитный монополь пятьдесят лет спустя, пер. с англ., "УФН", 1984, т. 144, с. 277. А. Д. Долгов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.