- МАГНИТНАЯ СИММЕТРИЯ
- МАГНИТНАЯ СИММЕТРИЯ
-
- раздел симметрии кристаллов, учитывающий специфику их магнитных свойств, а именно: в М. с. принимается во внимание симметрия уравнений движения по отношению к операции обращения времени R, под действием к-poii координаты всех точек кристалла остаются неизменными, а скорости меняются на противоположные. Соответственно, под действием операции R средняя по времени микроскопическая плотность заряда
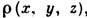описывающая обычную (электрическую) структуру кристалла, не меняется, и кроме р рассматривается микроскопическая средняя плотность магнитного момента 
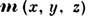[или, что эквивалентно, тока 
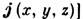, меняющая знак под действием R. Группой магнитной симметрии кристалла называется множество преобразований (пространственных и комбинаций из R и пространственных преобразований), оставляющих инвариантными функции 
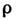( х, у,z) и m ( х, у,r). Если представить операцию R как замену чёрного цвета на белый, то магнитные группы совпадают с шубниковскими группами симметрии и антисимметрии.
Имеются три типа магнитных групп.
1. Для кристаллов без магнитной структуры m(x,y,
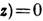, группа магнитной симметрии 
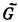содержит операцию Л и является прямым произведением пространственной (см. Фёдоровские группы )группы G на группу, состоящую из операции Л и тождественной операции 
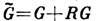(серые группы).
2. Белые группы вообще не содержат операции R и совпадают с фёдоровскими группами.
3. Чёрно-белые группы содержат операцию Л только в комбинациях
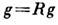с пространственными преобразованиями g, отличными от тождественного преобразования. Наиболее простой вывод чёрно-белых групп состоит в следующем: берётся фёдоровская группа G и её вещественное неединичное одномерное неприводимое представление; те элементы 
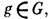для к-рых характеры 
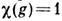, входят в шубниковскую группу 
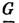непосредственно, а те, для к-рых 
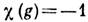,- в комбинации Rg. Перебирая все фёдоровские группы и их одномерные вещественные неединичные неприводимые представления, получаем все чёрно-белые шубниковские группы.
Всего имеется 1651 магнитная (шубниковская) пространственная группа, из них 230 серых, столько же белых и 1191 чёрно-белая. Для анализа макроскопических свойств достаточно ограничиться точечной симметрией. Всего имеется 122 кристаллографических магнитных класса (точечные группы), из них 32 серых, 32 белых и 58 чёрно-белых.
Среди макроскопических магнитных свойств особое место занимает намагниченность М. Любой магнитный класс, допускающий намагниченность, есть подгруппа группы симметрии магнитного момента
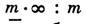(обозначения по Шубникову), состоящей из оси бесконечного порядка 
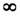(вдоль М), перпендикулярной ей плоскости симметрии т, а также бесконечного числа проходящих через ось оо антиплоскостей симметрии т (т. е. плоскостей отражения с одновременным обращением времени) и перпендикулярных оси оо антиосей второго порядка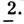 
Магнитное упорядочение возникает вследствие взаимодействий, зависящих от магнитного момента. Если пренебречь слабыми релятивистскими взаимодействиями, то остаётся обменное взаимодействие, зависящее от взаимной ориентации спинов и не зависящее от ориентации спинов относительно решётки. Поэтому кроме приведённого точного описания М. с. для классификации магнитных структур используется обменная симметрия (ОС). Группа ОС связана с группой G симметрии плотности заряда соотношением
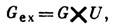
где U - группа вращений в спиновом пространстве. Поскольку в ОС ориентация спинов относительно решётки условна, можно считать, что под действием
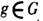спины ведут себя как скаляры и т(r )переходит в 
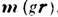. Действуя на т(r )различными 
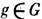, получаем представление группы G. Разлагая это представление на неприводимые, получаем
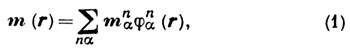
где п - номер представления,
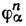- базисные функции представления. Функция m2(r) является спиновым инвариантом, поэтому она инвариантна относительно G и
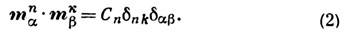
Максимальное число взаимно перпендикулярных компонент магн. момента равно 3, поэтому суммарная размерность представлений, входящих в разложение (1), не превышает трёх.
Классификация магнитных структур в ОС проводится перебором различных представлений фёдоровских групп. Если разложение (1) содержит только единичное представление, то имеется ферромагнитная структура, если не содержит единичного представления,- антиферромагнитная, в остальных случаях - ферримагнитная структура.
Если представить различные значения спина различными цветами, то ОС сводится к цветной симметрии (P -симметрия).
Лит.: Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982; Копцик В. А., Шубниковские группы, М., 1966; Андреев А. Ф., Марченко В. И., "ЖЭТФ", 1976, т. 70, с. 1522, Замор заев А. М., Галярский Э. И., Палистрант А. Ф., Цветная симметрия, ее обобщения и приложения, Кишинев, 1978; Изюмов Ю. А., Найш В. Е., Озеров Р. П., Нейтронография магнетиков, М., 1981. Е. <Б. <Логинов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
