КОГЕРЕНТНОЕ СОСТОЯНИЕ

КОГЕРЕНТНОЕ СОСТОЯНИЕ

квантового осциллятора - состояние, максимально близкое к состоянию классич. осциллятора в том смысле, что произведение неопределённостей (дисперсий) координаты и импульса в этом состоянии принимает минимально возможное в рамках неопределённостей соотношения значение. Термин введён Р. Глаубером [1]. С аналогичным свойством волновые пакеты строились в начале развития квантовой механики Э. Шрёдингером [2]. В К. с. гармонич. осциллятора волновой пакет не расплывается, а его центр движется по классической траектории.

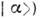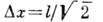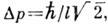Дисперсии координаты и импульса одномерного квантового гармонич. осциллятора в К. с. (с вектором состояния равны соответственно и где l - амплитуда нулевых колебаний, так что 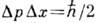. При этом изменение во времени ср. значений координаты и импульса соответствует классич. траекториям, а 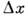и 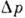остаются постоянными, т. е., эволюционируя, К. с. остаётся когерентным.

К. с. 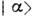осциллятора массы т и частоты 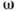описывается нормированной волновой ф-цией, имеющей в координатном представлении вид гауссова волнового пакета (см. Гаусса распределение):

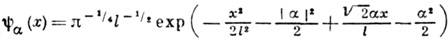
Здесь 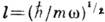, 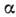- любое комплексное число, действит. часть к-рого связана со ср. значением оператора координаты 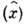в состоянии 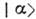: 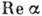= =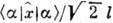, а мнимая - со ср. значением оператора нмпульса 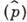: 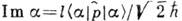. Т. о., положение центра х _с гауссова пакета в К. с. определяется числом 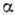: 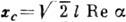. В импульсном представлении волновая ф-ция К. с. также имеет вид гауссова пакета:

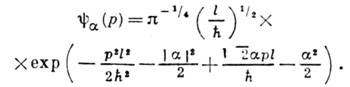
Вместо операторов 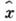и 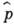удобно ввести операторы уничтожения 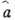и рождения :

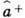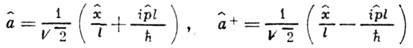
(крест означает эрмитово сопряжение). Название операторов связано с тем, что действие 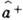на состояние 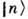гармонич. осциллятора с заданной энергией 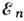= = 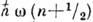(n=0, 1, 2, . . .) переводит осциллятор в возбуждённое состояние 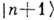, увеличивая его энергию на квант энергии 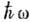, а действие 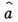на 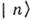уменьшает его энергию на этот же квант.

К. с. 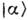является собственным состоянием оператора уничтожения:

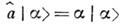
Оно получается действием унитарного оператора 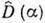= =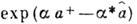на вектор осн. (вакуумного) состояния 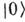, 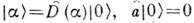(звёздочкой помечено комплексное сопряжение).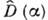наз. оператором сдвига, т. к. он смещает центр волнового пакета на величину

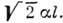
Скалярное произведение двух векторов К. с. (или матричный элемент единичного оператора в представлении К. с.) имеет вид

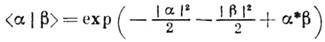
и не равно нулю при 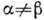, т. е. К. с. неортогональны. Однако квадрат модуля скалярного произведения

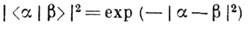
очень быстро стремится к нулю при 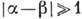, что физически отвечает уменьшению перекрытия двух волновых пакетов, центры к-рых раздвигаются (поскольку 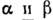определяют центры этих пакетов). По состояниям 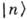с заданной энергией К. с. разлагается в ряд:

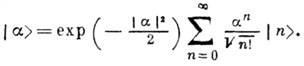
Это означает, что ехр 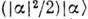является производящей ф-цией для состояний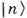

Ср. значение энергии осциллятора в К. с. 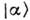определяется ф-лой

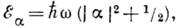
а распределение по уровням энергии является распределением Пуассона:

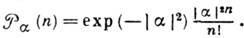
При этом эволюция К. с. задаётся ф-лой

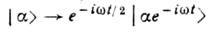
К. с. 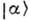образуют полную, точнее переполненную, систему векторов состояний; разложение единичного оператора 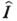имеет вид

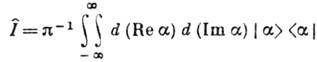
Произвольный вектор состояния 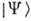может быть разложен по К. с.:

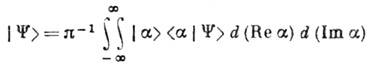
В квантовой теории поля система частиц с целым спином - бозонов (фотонов, 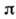-мезонов и т. д.) - описывается как бесконечный набор квантовых гармонич. осцилляторов. Возбуждённому состоянию осциллятора 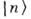отвечает при этом совокупность п бозонов с энергией 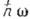. В этом случае оператор уничтожения а уменьшает, а оператор рождения 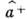увеличивает число частиц в системе на единицу.

К. с. квантованного эл.-магн. поля (и других бозе-полей) вводятся на основе представления гамильтониана поля в виде суммы гамильтонианов гармонич. осцилляторов, отвечающих разл. модам колебаний поля. Для моды определ. частоты и поляризации эл.-магн. поля К. с. описывается приведёнными выше ф-лами, при этом в К. с. число фотонов неопределённо, а распределение по числу фотонов является распределением Пуассона. Если все осцилляторы поля находятся в К. с., то состояние квантового поля наиб. близко к классическому.

Важность К. с. в физике обусловлена тем, что во мн. случаях физ. квантованные поля находятся именно в таких состояниях. Напр., классич. ток, срздавае-мый движущимися электрич. зарядами, излучает фотоны, находящиеся в К. с. Инфракрасная расходимость в квантовой электродинамике объясняется и устраняется учётом того, что квантованное поле в случае малых частот находится в К. с. При точном квантовомеха-нич. описании когерентных источников света с необходимостью возникают К. с. эл.-магн. поля. Свойства сверхтекучести и сверхпроводимости также могут быть объяснены тем, что соответственно сверхтекучая компонента в жидком гелии и куперовские пары в сверхпроводниках находятся в К. с. Это же относится и к др. явлениям с упорядочением.

Для произвольных квантовых систем с N степенями свободы К. с. вводятся по след. схеме. Находятся N неэрмитовых интегралов движения 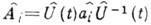с бозонными коммутац. соотношениями 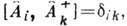где 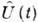- оператор эволюции системы, переводящий вектор состояния, заданный в нач. момент времени, 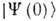, в вектор состояния 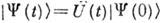; 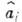- оператор уничтожения, действит. и мнимая части к-рого определяют нач. точку траектории системы в фазовом пространстве ср. координат и импульсов ( 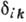- символ Кронекера). Затем находится нормированный вакуумный вектор (вектор осн. состояния) из решения системы ур-ний 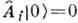. Действием на этот вектор оператора сдвига строится К. с.:

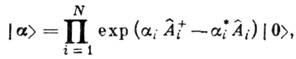
удовлетворяющее временному ур-нию Шрёдингера. Для квантовых систем общего вида ср. изменения координат и импульсов, вообще говоря, не соответствуют классич. траекториям, а волновые ф-ции в К. с. являются гауссовыми пакетами только в нач. момент времени - произведение неопределённостей координаты и импульса не остаётся со временем равным

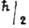
Однако существенным для расчётов является свойство К. с. быть производящей ф-цией для состояний - аналогов состояний с заданной энергией стационарного квантового осциллятора. Как пример для квантовых систем, описываемых нестационарным гамильтонианом квадратичной формы по операторам координат и импульсов, это свойство позволяет найти точно (не по теории возмущений) через многомерные полиномы Эрмита вероятности переходов между уровнями энергии N -мерного гармонич. осциллятора при параметрич. возбуждении самого общего типа [3].

Особым видом К. с. являются т. н. с ж а т ы е (squeezed) К. с. В этих состояниях волновые пакеты - гауссовы, по 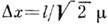, , 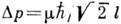где 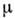- любое положит. число; при этом по-прежнему 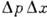= 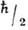Такие состояния важны, напр., при попытках (пока не реализованных) построить детекторы гравитац. волн интерференц. типа.

Лит.:1) Glauber R. J., Photon correlations, "Phys. Rev. Lett.", 1963, v. 10, p. 84; 2) S с h r o d i n g e r E., Der stetige Ubergang von der Mikro- zur Makromechanik, "Naturwiss.", 1926, Bd 14, S. 664; 3) M а л к и н И. А., М а н ь к о В. И., Динамические симметрии и когерентные состояния квантовых систем, М., 1979; 4) Когерентные состояния в квантовой теории. Сб. ст., пер. с англ., М., 1972. В. И. Манько.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.