КВАЗИПОТЕНЦИАЛЬНЫЙ ПОДХОД

КВАЗИПОТЕНЦИАЛЬНЫЙ ПОДХОД

в квантовой теории поля - метод трёхмерного описания системы неск. частиц в релятивистской квантовой теории. Предложен А. А. Логуновым и А. Н. Тавхелидзе в 1962. Осн. идеи метода проще всего проследить на примере системы двух частиц. В квантовой теории поля (КТП) такая система может быть описана в рамках ковариантного четырёхмерного формализма на основе Бете - Солпитера уравнения для четырёхвременной Грина функции и двухвременной волновой ф-ции двух частиц. В этом формализме каждой частице приписывается своё индивидуальное время, в результате чего волновая ф-ция не допускает обычного вероятностного толкования в духе нерелятивистской квантовой механики и крайне усложняется вопрос о граничных условиях по переменной относительного времени. Указанные трудности можно преодолеть, если ввести для всех частиц системы общий инвариантный временной параметр, направив ось времени по полному 4-импульсу системы. Такое трёхмерное одновременное описание будет явно ковариантным, поскольку полный 4-импульс замкнутой системы частиц сохраняется. Цель К. п., т. о., состоит в ковариантном обобщении потенц. теории взаимодействия двух (и более) частиц на релятивистский случай, где существенны неупругие процессы рождения и уничтожения частиц, а также зависимость взаимодействия от скоростей частиц. <В импульсном представлении релятивистская волновая ф-ция y_M,P( р) двух частиц удовлетворяет трёхмерному квазипотенц. ур-нию типа ур-ния Шрёдингера (в системе единиц ):

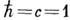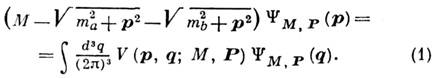
Здесь V - квазипотенциал, М - полная энергия двух частиц в системе отсчёта, в к-рой полный трёхмерный импульс двух частиц P=0, т. е. в системе центра масс (с. ц. м.). Т. о., М имеет смысл массы составной системы и является инвариантной величиной, а полная энергия в произвольной системе отсчёта P₀=S=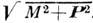 . Трёхмерные импульсы р и q имеют смысл относительных импульсов в с. ц. м. и могут быть ковариантным образом определены в любой системе отсчёта, m _а и m_b - массы частиц а и b.Ур-нию (1) можно дать простую трактовку - полная энергия (масса) составной системы слагается из энергии относит, движения свободных частиц и энергии их взаимодействия. В нерелятивистском пределе (p²/m² Ъ1)это ур-ние непосредственно переходит в обычное ур-ние Шрёдингера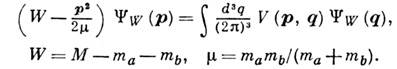

Квазипотенц. ур-ние достаточно решить в с. ц. м., поскольку волновая ф-ция в произвольной системеотсчёта (P№0) выражается простым образом через волновую ф-цию в с. ц. м.: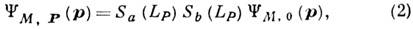

где S_a,b(L_P) - матрицы конечномерных представлений Лоренца группы, определяемые спиновыми свойствами частиц а и b (точнее, трансформац. свойствами соответствующих операторов поля), L_P- преобразование Лоренца, связывающее указанные выше системы отсчёта. Напр., для частиц со спином ¹/₂ матрица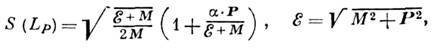

где a - Дирака матрицы. Переход в конфигурац. представление осуществляется с помощью трёхмерного преобразования Фурье. <Квазипотенциал V(p, q; M )определяется через амплитуду рассеяния двух частиц Т( р, q; М )вне энергетич. поверхности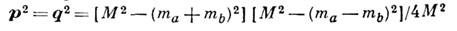

на основе трёхмерного ур-ния, аналогичного ур-нию для амплитуды рассеяния в нерелятивистской квантовой механике (в с. ц. м.):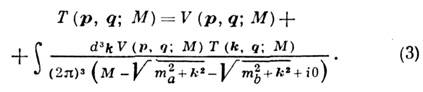

Отсюда V можно найти итерациями, напр., по теории возмущений, если V содержит малый параметр: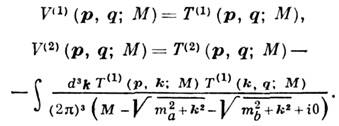

Ур-ние (3) обеспечивает, в частности, выполнение условия упругой (двухчастичной) унитарности для физ. амплитуды рассеяния на энергетич. поверхности (т. е. при учёте только вклада промежуточного упругого двухчастичного состояния). Квазипотенциал V в конфигурац. пространстве зависит от скорости и нелокален. Кроме того, он зависит от полной энергии системы и является, вообще говоря, комплексной ф-цией. Последние два свойства существенно отличают квазипотенциал от нерелятивистского потенциала. Так, зависимость от энергии приводит к более сложному условию нормировки волновой ф-ции связанного состояния: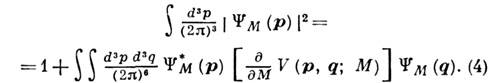

Мнимая часть квазипотенциала характеризует неупругие процессы в составной системе, знак её является строго определённым и соответствует условию поглощения .Предполагается, что амплитуда рассеяния Т( р, q; M) вне энергетич. поверхности может быть построена (хотя бы приближённо) в рамках КТП, напр., с помощью Фейнмана диаграмм в квантовой электродинамике. наиб. общим методом такого построения является использование т. н. двухвременных ф-ций Грина двух (и более) частиц, широко применяемых в статистич. физике. Приравнивание времён частиц в с. ц. м. эквивалентно в импульсном представлении интегрированию по переменной относит. энергии e в бесконечных пределах. В результате искомая амплитуда рассеяния выражается через четырёхвременную двухчастичнуюф-цию Грина G, используемую в методе Бете - Солпитера (импульсы частиц обозначены на рис.):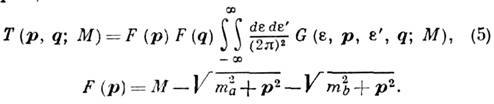

Другим, в нек-рых случаях более простым методом построения является частичный переход на массовую поверхность, где нужно положить e=e'=0 или перевести на массовую поверхность 4-импульс одной из частиц (напр., p_b²=q_b²=m_b²).В рамках К. п. могут быть рассмотрены как процессы рассеяния (М/m _а+m_b),так и связанные состояния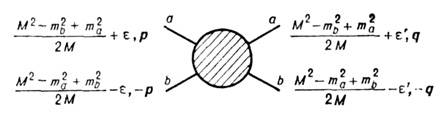

Параметризация 4-импульсов частиц в упругом процессе а+b "а+b.(М<m _а+m_b) двух (и более) частиц. При этом связанные состояния проявляются как полюсы двухвременной ф-ции Грина и амплитуды рассеяния. Квазипотенц. ур-ние (1) широко применяется для расчёта спектра энергии водородоподобных атомов: сверхтонкого расщепления осн. уровня энергии атомов водорода, мюония (е ^-m⁺) и позитрония (е ^- е ⁺); тонкой структуры, включая лэмбовский сдвиг, уровни энергии атома водорода и водородоподобных мюонных атомов. Ур-ние (1) успешно применяется для описания т. н. кваркония - связанного состояния тяжёлых кварка и антикварка. К. п. используется для описания поведения составных систем частиц во внеш. эл.-магн. полях. С высокой степенью точности найден магн. момент водородоподобного атома. Получено представление для матричных элементов локальных операторов токов между связанными состояниями в терминах квазипотенц. волновых ф-ций. В рамках составной кварковой модели адронов найдены асимптотич. выражения для эл.-магн. формфакторов адронов и структурных функций глубоко неупругого лептон-адронного рассеяния при высоких энергиях, исследовано поведение сечений инклюзивных процессов множественного рождения при высоких энергиях и больших передачах импульса. В рамках К. п. изучается также ряд вопросов релятивистской ядерной физики. Все полученные результаты хорошо согласуются с эксперим. данными. <Ур-ние (3) с заданным феноменологич. квазипотенциалом конечного радиуса применяется для изучения бинарных (в т. ч. упругих) реакций адронов при высоких энергиях. Выбирая квазипотенциал в виде гладкой, локальной (в конфигурац. пространстве) ф-ции, зависящей от энергии, с положительно определённой мнимой частью, удаётся правильно описать осн. свойства рассеяния адронов на малые и большие углы. Лит.:Логунов А. А., Тавхелидзе А. Н., Фаустов Р. Н., Квазипотенциальный подход в квантовой теории поля, в кн.: XII Международная конференция по физике высоких энергий, т. 1, М., 1966, с. 222; Кадышевский В. Г., Тавхелидзе А. Н., Квазипотенциальный метод в релятивистской задаче двух тел, в кн.: Проблемы теоретической физики, М., 1969, с. 261; Гарсеванишвили В. Р., Матвеев В. А., Слепченко Л. А., Рассеяние адронов при высоких энергиях и кваэипотенциальный подход в квантовой теории поля, "ЭЧАЯ", 1970, т. 1, с. 91; Фаустов Р. Н., Уровни энергии и электромагнитные свойства водородоподобных атомов, там же, 1972, т. 3, с. 238; Квинихидзе А. Н. и др., Инклюзивные процессы с большими поперечными импульсами в подходе составных частиц, там же, 1977, т. 8, с. 478. Р. Н. Фаустов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.