КВАЗИКООРДИНАТЫ

- понятия, устанавливаемые след. образом: если положение механич. системы определяется s обобщёнными координатами q₁, q₂,..., q_s,то величины dp₁, dp₂, ..., dp_s, являющиеся независимымидруг от друга линейными комбинациями дифференциалов координат q₁, q₂,...,q_s и выражаемые неинтегрируемыми равенствами вида

dp_i=a_i1dq₁+а _i2dq₂+. . .+ a_isdq_s(i= 1,2, . .., s) (1)

(где а_ik- коэф., зависящие от q_l,q₂,..., q_s),наз. дифференциалами К., а сами p₁, p₂,...,p_s - К. данной системы. Поскольку ур-ния (1) неинтегрируемы, то явных выражений для К. p_i как функций q_l,q₂,...,q_s не существует. Если же ур-ния (1) могут быть проинтегрированы и из них можно определить p_i как ф-ции q_l, q₂,...,q_s,то p_i будут в этом случае не К., а нек-рыми новыми обобщёнными координатами системы. По аналогии величины

(где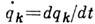 - обобщённые скорости, t - время) наз. квазискоростями. Поскольку явных выражений для К. p_i не существует, то w_i, в отличие от обобщённых (истинных) скоростей, не представляют собою производных по времени от к.-н. координат (параметров), а символ dp_i/dtв равенствах (2) является лишь условным обозначением. <Использование К. и квазискоростей позволяет в ряде случаев существенно упростить вид соответствующих ф-л и ур-ний, а также выкладок, связанных с их получением. Напр., для твёрдого тела, движущегося вокруг неподвижной точки О, <проекции его мгновенной угл. скорости на связанные с телом оси Oxyz,если за обобщённые координаты принять Эйлера углыj, y, q, имеют значения (см. Эйлера кинематические уравнения):

Эти ур-ния, по виду аналогичные равенствам (2), не могут быть проинтегрированы и из них нельзя определить p₁, p₂, p₃ как ф-ции j, y, q. Следовательно, p₁, p₂, p₃ будут в данном случае соответствующими К., а w₁, w₂, w₃ - квазискоростями, к-рые не могут быть выражены в виде производных по времени от к.-н. величин. Но используя w₁, w₂, w₃ и приняв одновременно за оси Oxyzгл. оси инерции тела для точки О, <можно, напр., получить очень компактное выражение для кинетич. энергии Т тела: T=0,5(I₁w₁²+I₂w₂²+I₃w₃²), где I₁, I₂, I₃ - моменты инерции тела относительно осей х, у,z соответственно. Из равенств (3) видно, каким громоздким будет ур-ние для Т, <выраженное непосредственно через координаты j, y, q и скорости . Если же в данном случае воспользоваться ур-ниями Лагранжа в К. (см. [2]), то в них вместо производных от Т по обобщённым скоростям войдут производные по квазискоростям w₁, w₂, w₃, имеющие, как видно, очень простые выражения (РT/Рw₁=I₁w₁ и т. д.), а производные по К. p₁, p₂, p₃ обратятся в нули; в результате получаются очень компактные дифференц. ур-ния движения тела вокруг точки О(см. Эйлера динамические уравнения). Лит.:1) Уиттекер Е. Т., Аналитическая динамика, пер. с англ., М.- Л., 1937, p 30; 2) Лурье А. И., Аналитическая механика, М., 1961. С. М. Тaрг.