СУПЕРПОЗИЦИИ ПРИНЦИП

СУПЕРПОЗИЦИИ ПРИНЦИП

       

(наложения принцип),

1) допущение, согласно к-рому результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что последние взаимно не влияют друг на друга. С. п. строго применим к системам, поведение к-рых описывается линейными соотношениями (т. н. линейные системы). Напр., если среда, в к-рой распространяется волна S, линейна, т. е. её св-ва не меняются под действием возмущений, создаваемых волной, то все эффекты, вызываемые негармонич. волной, могут быть определены как сумма эффектов, создаваемых каждой из её гармонич. составляющих: S=S1+S2+S3+. . . С. п. играет большую роль в теории колебаний, теории цепей и др. разделах физики и техники.

2) В теории классич. полей и в квант. теории — положение, согласно к-рому суперпозиция (т. е. результат суммирования, наложения друг на друга) любых допустимых в данных условиях состояний физ. системы (или возможных процессов в ней) явл. также допустимым состоянием (или соответственно возможным процессом). Так, классич. эл.-магн. поле в вакууме удовлетворяет С. п.: сумма любого числа физически реализуемых полей есть также физически реализуемое эл.-магн. поле. В силу С. п. эл.-магн. поле, созданное совокупностью электрич. зарядов и токов, равно сумме полей, создаваемых этими зарядами и токами по отдельности. Слабое гравитац. поле также с хорошей точностью подчиняется С. п.

В классич. физике С. п.— приближённый принцип, вытекающий из линейности ур-ний движения соответствующих систем (что обычно явл. хорошим приближением для описания реальных систем), напр. Максвелла уравнений для эл.-магн. поля. Т. о., он вытекает из более глубоких динамич. принципов и. поэтому не явл. фундаментальным. Он и не универсален. Так, достаточно сильное гравитац. поле не удовлетворяет С. п., поскольку оно описывается нелинейными ур-ниями Эйнштейна (см. ТЯГОТЕНИЕ); макроскопич. эл.-магн. поле в в-ве, строго говоря, также не подчиняется С. п. в силу зависимости (иногда существенной) диэлектрич. и магн. проницаемостей от внеш. поля (напр., в ферромагнетике) и т. д.

В квант. механике С. п.— фундам. принцип, один из осн. постулатов, определяющий вместе с неопределённостей соотношением структуру матем. аппарата теории. Из С. п. следует, что состояния квантовомеханич. системы должны изображаться векторами линейного пр-ва (см. КВАНТОВАЯ МЕХАНИКА), в частности волновыми функциями; что операторы физ. величин должны быть линейными и т. д. С. п. утверждает, что если квантовомеханич. система может находиться в состояниях, описываемых волн. ф-циями y1, y2, . . ., yn, то физически допустимой будет и суперпозиция этих состояний, т. е. состояние, изображаемое волн. ф-цией:

y=c1y1+c2y2 +...+ сnyn, (*)

где c1, с2, . . ., сn — произвольные комплексные числа. Из С. п. следует, что любая волн. ф-ция может быть разложена в сумму (вообще говоря, бесконечную) собств. ф-ций оператора любой физ. величины; при этом квадраты модулей коэфф. в разложении имеют смысл вероятностей обнаружить на опыте соответствующие значения этой величины. Суперпозиция состояний (*) определяется не только модулями коэфф. ci, но и их относит. фазами, поэтому она означает интерференцию состояний yi. Возможность такой интерференции проявляется, напр., в дифракции микрочастиц. Квант. С. п. лишён наглядности, характерной для С. п. в классич. физике, т. к. в квант. теории в суперпозиции участвуют (складываются) альтернативные, с классич. точки зрения взаимоисключающие друг друга, состояния. С. п. отражает волн. природу микрочастиц.

В релятив. квант. теории, рассматривающей процессы, в к-рых могут происходить взаимопревращения ч-ц, С. п. должен быть дополнен т. н. правилами суперотбора. Напр., суперпозиции состояний с разными значениями электрического, барионного, лептонного зарядов физически не реализуемы: их существование означало бы, что при измерении, напр., электрич. заряда квант. системы можно с определ. вероятностью получить разные его значения, что противоречит опыту. Поэтому операторы физ. величин не должны менять заряды. Это накладывает на матричные элементы операторов определ. ограничения, к-рые и наз. правилами суперотбора.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

СУПЕРПОЗИЦИИ ПРИНЦИП

(наложения принцип) - 1) допущение, согласно к-рому результирующий эффект воздействия неск. процессов (напр., колебательных) представляет собой сумму эффектов, вызываемых воздействием каждого процесса в отдельности, при условии, что последние взаимно не влияют друг на друга. С. п. строго применим лишь к системам, поведение к-рых описывается линейными соотношениями (т. н. линейные системы). Напр., если среда, в к-рой распространяется волна, линейна, т. е. её свойства не меняются под действием возмущений, создаваемых волной, то все эффекты, вызываемые негармонич. волной, могут быть определены как сумма эффектов, создаваемых каждой из её гармонич. составляющих. С. п. играет большую роль в теории колебаний, теории цепей и др. разделах физики и техники.

В. В. Мигулин.

2) В теории классич. полей и в квантовой теории С. п.- положение, согласно к-рому суперпозиция (т. е. результат суммирования, наложения друг на друга) любых допустимых в данных условиях состояний физ. системы (или возможных процессов в ней) является также допустимым состоянием (или соответственно возможным процессом). Так, классич. эл.-магн. поле в вакууме удовлетворяет С. п.: сумма любого числа физически реализуемых полей есть также физически реализуемое эл.-магн. поле. В силу С. п. эл.-магн. поле, созданное совокупностью электрич. зарядов и токов, равно сумме полей, создаваемых этими зарядами и токами по отдельности. Слабое гравитац. поле также с хорошей точностью подчиняется С. п.

В классич. физике С. п.- приближённый, он вытекает из линейности ур-ний движения соответствующих систем (что обычно является хорошим приближением для описания реальных систем), напр. Максвелла уравнений для эл.-магн. поля в пустоте. При отклонениях от линейности обнаруживаются нарушения С. п. Так, достаточно сильное гравитац. поле не удовлетворяет С. п., поскольку оно описывается нелинейными ур-ниями Эйнштейна (см. Тяготение); макроскопическое эл.-магн. поле в веществе, строго говоря, также не подчиняется С. п. в силу зависимости (иногда существенной) диэлектрич. и магн. проницаемостей от внеш. поля (напр., в ферромагнетике, лазерных материалах) и т. д.

В квантовой механике С. п.- фундам. принцип, один из осн. постулатов, определяющий вместе с неопределённостей соотношением структуры матем. аппарата теории. Из С. п. следует, что состояния квантовомеханич. системы должны изображаться векторами линейного пространства (см. Квантовая механика), в частности волновыми функциями, что операторы физ. величин должны быть линейными и т. д. С. п. утверждает, что если квантовомеханич. система может находиться в состояниях, описываемых волновыми ф-циями y₁, y₂,..., y_n, то физически допустимой будет и суперпозиция этих состояний, т. е. состояние, описываемое волновой ф-цией:

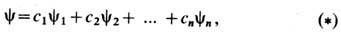
где с₁, с₂,..., с _п- произвольные комплексные числа. Из С. п. следует, что любая волновая ф-ция может быть разложена в сумму (вообще говоря, бесконечную) собств. ф-ций оператора любой физ. величины; при этом квадраты модулей коэф. в разложении имеют смысл вероятностей обнаружить на опыте соответствующие значения этой величины. Суперпозиция состояний (*) определяется не только модулями коэф. с _n, но и их относит. фазами, поэтому она означает интерференцию состояний y_n. Возможность такой интерференции проявляется, напр., в дифракционном рассеянии микрочастиц. Квантовый С. п. лишён наглядности, характерной для С. п. в классич. физике, т. к. в квантовой теории в суперпозиции участвуют (складываются) альтернативные, с классич. точки зрения взаимоисключающие друг друга, состояния. С. п. отражает волновую природу микрочастиц.

В релятивистской квантовой теории, рассматривающей процессы, в к-рых могут происходить взаимопревращения частиц, С. п. должен быть дополнен т. н. суперотбора правилами. Напр., суперпозиции состояний с разными значениями электрического, барионного, лептонного зарядов физически не реализуемы, их существование означало бы, что при измерении, напр., электрич. заряда квантовой системы можно с определ. вероятностью получить разные его значения, что противоречит опыту. Поэтому операторы физ. величин не должны менять заряды. Это накладывает на матричные элементы операторов определ. ограничения, к-рые и наз. правилами суперотбора.

Лит. см. при ст. Квантовая механика. О. И. Завьялов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.