ТЯГОТЕНИЕ

ТЯГОТЕНИЕ

       

(гравитация, гравитационное взаимодействие), универсальное взаимодействие между любыми видами материи. Если это вз-ствие относительно слабое и тела движутся медленно (по сравнению со скоростью света с), то справедлив закон всемирного тяготения Ньютона. В общем случае Т. описывается созданной А. Эйнштейном общей теорией относительности. Эта теория описывает Т. как воздействие материи на св-ва пр-ва и времени; в свою очередь, эти св-ва пространства-времени влияют на движение тел и др. физ. процессы. Т. о., совр. теория Т. резко отличается от теорий др. видов вз-ствия — эл.-магн., сильного и слабого. (Однако в настоящее время большинство физиков считает, что при очень высоких энергиях все виды фундаментальных вз-ствий объединяются в единое вз-ствие; (см. КВАНТОВЫЕ ЭФФЕКТЫ)

Теория тяготения Ньютона.

Первые высказывания о Т. как всеобщем св-ве тел относятся к античности. В 16 и 17 вв. в Европе возродились попытки доказательства существования взаимного тяготения тел. Нем. астроном И. Кеплер говорил, что «тяжесть есть взаимное стремление всех тел». Окончат. формулировка закона всемирного Т. была сделана Ньютоном в 1687 в гл. его труде «Математические начала натуральной философии». Закон тяготения Ньютона гласит, что две любые материальные ч-цы с массами mA и mB притягиваются по направлению друг к другу с силой F, прямо пропорц. произведению масс и обратно пропорц. квадрату расстояния r между ними:

F=GmAmB/r2 (1)

(под материальными ч-цами здесь понимаются любые тела при условии, что их линейные размеры много меньше расстояния между ними). Коэфф. пропорциональности G наз. гравитационной постоянной. Числовое значение G было определено впервые англ. учёным Г. Кавендишем в 1798, измерившим в лаборатории силы притяжения между двумя шарами. По совр. данным, (G=6,6745 (8) •10-8 см3/г•с2=6,6745 (8) •10-11 м3/кг•с2. Согласно закону (1), сила Т. зависит только от положения ч-ц в данный момент времени, т. е. гравитац. вз-ствие распространяется мгновенно.

Чтобы вычислить силу Т., действующую на данную ч-цу со стороны мн. др. ч-ц (или непрерывно распределённого в-ва в нек-рой области пр-ва), следует векторно сложить силы, действующие со стороны каждой ч-цы (проинтегрировать в случае непрерывного распределения в-ва). Т. о., в ньютоновской теории Т. справедлив суперпозиции принцип. Ньютон теоретически доказал, что сила Т. между двумя шарами конечных размеров со сферически симметричным распределением в-ва выражается также ф-лой (1), где mA и mB — полные массы шаров, a r — расстояние между их центрами. При произвольном распределении в-ва сила Т., действующая в данной точке на пробную ч-цу, может быть выражена как произведение массы этой ч-цы на вектор g, наз. напряжённостью поля Т. в данной точке. Чем больше по модулю g, тем сильнее поле Т.

Из закона Ньютона следует, что поле Т.— потенц. поле, т. е. его напряжённость g может быть выражена как градиент нек-рой скалярной величины j, наз. гравитационным потенциалом:

g=- gradj. (2)

Так, для ч-цы массы т потенциал поля Т.

j=-Gm/r. (3)

Если задано произвольное распределение плотности в-ва в пр-ве r=r(r), то можно вычислить гравитац. потенциал j этого распределения, а следовательно, и напряжённость гравитац. поля g во всём пр-ве. Потенциал j определяется как решение Пуассона уравнения:

Dj = 4pGr, (4)

где D=d2ldx2+d2/dy2+d2/dz2 — оператор Лапласа.

Гравитац. потенциал к.-л. тела или системы тел может быть записан в виде суммы потенциалов полей Т. частичек, слагающих тело или систему (принцип суперпозиции), т. е. в виде интеграла от выражения (3):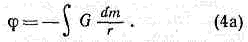

Интегрирование производится по всей массе тела (или системы тел), r — расстояние элемента массы dm от точки, в к-рой вычисляется потенциал. Выражение (4а) явл. решением ур-ния Пуассона (4). Потенциал изолиров. тела (системы тел) определяется неоднозначно. Напр., к потенциалу можно прибавлять произвольную константу. Однако если потребовать, чтобы вдали от тела, на бесконечности, потенциал равнялся нулю, то потенциал определяется решением ур-ния Пуассона однозначно в виде (4а).

Ньютоновская теория Т. и ньютоновская механика явились величайшим достижением естествознания. Они позволяют описать с большой точностью обширный круг явлений, в т. ч. движение естеств. и искусств. тел в Солнечной системе, движения в др. системах небесных тел: в двойных звёздах, в звёздных скоплениях, в, галактиках. На основе теории тяготения Ньютона было предсказано существование планеты Нептун и спутника Сириуса и сделаны мн. др. предсказания, впоследствии блестяще подтвердившиеся. В астрономии закон тяготения Ньютона явл. фундаментом, на основе к-рого вычисляются движения и строение небесных тел, их эволюция, определяются массы небесных тел. Точное определение гравитац. поля Земли позволяет установить распределение масс под её поверхностью (гравиметрич. разведка). Однако в нек-рых случаях Т. не может быть описано законом Ньютона.

Необходимость обобщения закона тяготения Ньютона.

Теория Ньютона предполагает мгновенное распространение Т. и уже поэтому не может быть согласована со спец. теорией относительности (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ), утверждающей, что никакое вз-ствие не может распространяться со скоростью, превышающей скорость света в вакууме. Определим условия, ограничивающие применимость ньютоновской теории Т. Так как эта теория не согласуется со спец. теорией относительности, то её нельзя применять в тех случаях, когда гравитац. поля настолько сильны, что разгоняют движущиеся в них тела до скоростей порядка скорости света с. Скорость, до к-рой разгоняется тело, свободно падающее из бесконечности (предполагается, что там оно имело пренебрежимо малую скорость) до нек-рой точки, равна по порядку величины квадратному корню из модуля гравитац. потенциала j в этой точке (предполагается, что на бесконечности j=0). Т. <о., теорию Ньютона можно применять только в том случае, если

|j|<-с2. (5)

В полях Т. обычных небесных тел это условие выполняется; так, на поверхности Солнца |j|/с2»4•10-6, а на поверхности белых карликов — порядка 10-3.

Ньютоновская теория неприменима также к расчёту движения ч-ц даже в слабом поле Т., удовлетворяющем условию (5), если ч-цы, пролетающие вблизи массивных тел, уже вдали от этих тел имели скорость, сравнимую со скоростью света. В частности, теория Ньютона неприменима для расчёта траектории света в поле Т. Наконец, теория Ньютона неприменима при расчётах перем. поля Т., создаваемого движущимися телами (напр., двойными звёздами) на расстояниях r>l=ct, где t — характерное время движения в системе (напр., период обращения в системе двойной звезды). Действительно, согласно ньютоновской теории, поле Т. на любом расстоянии от системы определяется положением масс в тот же момент времени, в к-рый определяется поле, т. е. изменения гравитац. поля, связанные с перемещением тел в системе, мгновенно передаются на любое расстояние r, что противоречит спец. теории относительности.

Обобщение теории Т. на основе спец. теории относительности было сделано Эйнштейном в 1915—16. Новая теория была названа им общей теорией относительности (ОТО).

Принцип эквивалентности.

Самой важной особенностью поля Т., известной в ньютоновской теории и положенной Эйнштейном в основу новой теории, является то, что Т. совершенно одинаково действует на разные тела, сообщая им одинаковые ускорения независимо от массы, хим. состава и др. св-в тел. Так, на поверхности Земли все тела падают под влиянием её поля Т. с одинаковым ускорением — ускорением свободного падения. Этот факт был установлен опытным путём итал. учёным Г. Галилеем и может быть сформулирован как принцип строгой пропорциональности гравитационной, или тяжёлой, массы mт, определяющей вз-ствие тела с полем Т. я входящей в закон (1), и инертной массы mи, определяющей сопротивление тела действующей на него силе и входящей во второй закон механики Ньютона. Ур-ние движения тела в поле Т. записывается в виде:

mиа=F=mтg, (6)

где а — ускорение, приобретаемое телом под действием напряжённости гравитац. поля д. Если mи пропорц. mт и коэфф. пропорциональности одинаков для любых тел, то можно выбрать ед. измерения так, что этот коэфф. станет равен единице, mи =mт; тогда массы сокращаются в ур-нии (6) и ускорение а не зависит от массы и равно напряжённости g поля Т., в согласии с законом Галилея. (О совр. опытном подтверждении этого фундам. факта см. ниже.)

Т. о., тела разной массы 0 природы движутся в заданном поле Т. совершенно одинаково, если их нач. скорости одинаковы. Этот факт показывает глубокую аналогию между движением тел в поле Т. и движением тел в отсутствие Т., но относительно ускоренной системы отсчёта. Так, в отсутствие Т. тела разной массы движутся по инерции прямолинейно и равномерно. Если наблюдать эти тела, напр., из кабины косм. корабля, к-рый движется вне полей Т. с пост. ускорением за счёт работы двигателя, то по отношению к кабине все тела будут двигаться с пост. ускорением, равным по величине и противоположным по направлению ускорению корабля. Движение тел будет таким же, как падение с одинаковым ускорением в постоянном однородном поле Т. Силы инерции, действующие в ускоренном косм. корабле, летящем с ускорением, равным ускорению свободного падения у поверхности Земли, неотличимы от сил гравитации, действующих в истинном поле Т. в корабле, стоящем на поверхности Земли. Следовательно, силы инерции в ускоренной системе отсчёта (связанной с косм. кораблём) эквивалентны гравитац. полю. Этот факт выражается принципом эквивалентности Эйнштейна. Согласно этому принципу, можно осуществить и процедуру, обратную описанной выше имитации поля Т. ускоренной системой отсчёта, а именно — можно «уничтожить» в данной точке истинное гравитац. поле введением системы отсчёта, движущейся с ускорением свободного падения. Так, хорошо известно, что в кабине косм. корабля, свободно (с выключенными двигателями) движущегося вокруг Земли в её поле Т., наступает состояние невесомости — не проявляются силы Т. Эйнштейн предположил, что не только механич. движение, но и вообще все физ. процессы в истинном поле Т. и в ускоренной системе в отсутствии Т. протекают по одинаковым законам. Этот принцип получил назв. «сильного принципа эквивалентности», в отличие от «слабого принципа эквивалентности», относящегося только к законам механики.

Теория тяготения Эйнштейна.

Рассмотренная система отсчёта (косм. корабль с работающим двигателем), движущаяся с пост. ускорением в отсутствии поля Т., имитирует только однородное гравитац. поле, одинаковое по величине и направлению во всём пр-ве. Но поля Т., создаваемые отд. телами, не таковы. Чтобы имитировать, напр., сферич. поле Т. Земли, нужны ускоренные системы с разл. направлением ускорения в разл. точках. Наблюдатели в разных системах, установив между собой связь, обнаружат, что они движутся ускоренно друг относительно друга, и тем самым установят, что истинное поле Т. отсутствует. Т. о., истинное поле Т. не сводится просто к введению ускоренной системы отсчёта в обычном пр-ве, или, точнее, в пространстве-времени специальной теории относительности. Эйнштейн показал, что если, исходя из принципа эквивалентности, потребовать, чтобы истинное гравитац. поле было эквивалентно локальным соответствующим образом ускоренным в каждой точке системам отсчёта, то в любой конечной области пространство-время окажется искривлённым — неевклидовым. Это означает, что в трёхмерном пр-ве геометрия, вообще говоря, будет неевклидовой (сумма углов треугольника не равна я, отношение длины окружности к радиусу не равно 2я и т. д.), а время в разных точках будет течь по-разному. Т. о., согласно теории тяготения Эйнштейна, истинное гравитац. поле есть проявление искривления (отличия геометрии от евклидовой) четырёхмерного пространства-времени.

Следует подчеркнуть, что создание теории тяготения Эйнштейна стало возможным только после открытия неевклидовой геометрии Н. И. Лобачевским, венг. математиком Я. Больяй, нем. математиками К. Гауссом и Б. Риманом.

В отсутствии Т. в пространстве-времени спец. теории относительности движение тела по инерции изображается прямой линией, или, на матем. языке, экстремальной (геодезической) линией. Осн. идея эйнштейновской теории Т. заключается в том, что и в поле Т. все тела движутся по геодезич. линиям в пространстве-времени, к-рое, однако, искривлено, и, следовательно, геодезич. линии — не прямые. Наблюдатель воспринимает это движение как движение по искривлённым траекториям в трёхмерном пространстве-времени с перем. скоростью. В заданном поле Т. все тела независимо от их массы и состава при одинаковых начальных условиях будут двигаться по одним и тем же геодезич. линиям (т. е. совершенно одинаково). Поэтому изменение скорости любых тел, т. е. их ускорение, в данном гравитац. поле одинаково. Одинаковость ускорений тел любой массы означает строгую пропорциональность тяжёлой и инертной масс (см. ф-лу (6)), и эти массы неотличимы.

Кривизна пространства-времени создаётся источниками гравитац. поля. При этом Т., т. е. искривление пространства-времени, определяется не только массой в-ва, слагающего тело, но и всеми видами энергии, присутствующими в системе. Эта идея явилась обобщением на случай теории Т. принципа эквивалентности массы (т) и энергии (?) спец. теории относительности: ?=mc2. Согласно этой идее, Т. зависит не только от распределения масс в пр-ве, но и от их движения, от давления и натяжений, имеющихся в телах, от эл.-магн. поля и всех др. физ. полей.

Наконец, в теории тяготения Эйнштейна обобщается вывод спец. теории относительности о конечной скорости распространения всех видов вз-ствия. Согласно Эйнштейну, изменения гравитац. поля распространяются в вакууме со скоростью с.

Уравнения тяготения Эйнштейна. В спец. теории относительности в инерциальной системе отсчёта (и. с. о.) квадрат четырёхмерного «расстояния» в пространстве-времени (интервала ds) между двумя бесконечно близкими событиями записывается в виде:

ds2 = (cdt)2-dx2-dy2-dz2, (7)

где t — время, х, у, z — прямоугольные декартовы координаты. Эта система координат наз. галилеевой. Выражение (7) имеет вид, аналогичный выражению для квадрата расстояния в евклидовом трёхмерном пр-ве в декартовых координатах. Такое пространство-время называют плоским, евклидовым, или точнее, псевдоевклидовым, подчёркивая особый хар-р времени: в выражении (7) перед (cdt)2 стоит знак «+», в отличие от знаков «-» перед квадратами дифференциалов пространств. координат. Т. о., спец. теория относительности явл. теорией физ. процессов в плоском пространстве-времени (Минкоеского пространстве-времени). Однако в нём не обязательно пользоваться декартовыми координатами, в к-рых интервал записывается в виде (7). Можно ввести любые криволинейные координаты. Тогда ds2 будет выражаться через эти новые координаты общей квадратичной формой:

ds2=gikdxidxk (8)

(i, k=0, 1, 2, 3), где х1, х2, х3 — произвольные пространств. координаты, x0 — временная координата (здесь и далее по дважды встречающимся индексам производится суммирование). С физ. точки зрения переход к произвольным координатам означает и переход от и. с. о. к системе, вообще говоря, движущейся с ускорением (причём в общем случае разным в разных точках), деформирующейся и вращающейся, и использование в этой системе недекартовых координат (и произвольно идущих часов). Несмотря на кажущуюся сложность использования таких систем, практически они иногда оказываются удобными. Но в спец. теории относительности всегда можно пользоваться и галилеевой системой (7), в к-рой интервал записывается особенно просто (в этом случае в ф-ле (8) gik=0 при i?k, g00=l. gii=-1 при i=1, 2, 3).

В ОТО пространство-время не плоское, а искривлённое. В таком пространстве-времени (в конечных, не малых областях) нельзя ввести декартовы координаты, и использование криволинейных координат становится неизбежным. В конечных областях искривлённого пространства-времени ds2 записывается в криволинейных координатах в общем виде (8). Зная gik как ф-ции четырёх координат, можно определить все геом. св-ва пространства-времени. Говорят, что величины gik, определяют метрику пространства-времени, а совокупность всех gik называют метрическим тензором. С помощью gik вычисляются темп течения времени в разных точках системы отсчёта и расстояния между точками в трёхмерном пр-ве. Так, ф-ла для вычисления бесконечно малого интервала времени dt по часам, покоящимся в системе отсчёта, имеет вид: dt=?(g00dx0/c). При наличии поля Т. величина g00 в разных точках разная, следовательно, темп течения времени зависит от поля Т. Оказывается, что чем сильнее поле, тем медленнее течёт время по сравнению с течением времени для наблюдателя вне поля.

Матем. аппаратом ОТО явл. тензорное исчисление; её законы записываются в произвольных криволинейных координатах (это означает, в частности, запись в произвольных системах отсчёта), как говорят, в ковариантном виде. Осн. задача теории Т.— определение гравитац. поля, что соответствует в ОТО нахождению геометрии пространства-времени. Эта последняя задача сводится к нахождению метрич. тензора gik.

Ур-ния тяготения Эйнштейна связывают величины gik с величинами, характеризующими материю, создающую поле: плотностью, потоками импульса и т. п. Эти ур-ния записываются в виде:

Rik-1/2gikR=(8pG/c4)Tik. (9)

Здесь Rik — т. н. тензор Риччи, выражающийся через gik, его первые и вторые производные по координатам; R=Rikgik (величины gik определяются из ур-ний gikgkm =dmi, где dmi— символ Кронекера: dmi=1 при i=m,dmi=0 при i?m); Тik — тензор энергии-импульса материи, компоненты к-рого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физ. материей подразумевается обычное в-во и физ. поля).

Вскоре после создания ОТО Эйнштейн показал (1917), что существует возможность изменения ур-ний (9) с сохранением осн. принципов новой теории. Это изменение состоит в добавлении к правой части ур-ний (9) т. н. космологич. члена: Lgik. Постоянная Л наз. космологич. постоянной, имеет размерность см-2. Целью этого усложнения теории была попытка Эйнштейна построить модель Вселенной, к-рая не изменяется со временем. Космологич. член можно рассматривать как величину, описывающую плотность энергии и давление (или натяжение) вакуума. Однако в сер. 20-х гг. А. А. Фридман показал, что ур-ния Эйнштейна без L-члена приводят к эволюционирующей (нестационарной) модели Вселенной, а амер. астроном Э. Хаббл открыл (1929) закон красного смещения для галактик, к-рое было истолковано как подтверждение этой модели. Идея Эйнштейна о статич. Вселенной оказалась неверной, и хотя уравнения с L-членом тоже допускают нестационарные решения для модели Вселенной, необходимость в L-члене отпала. Следует подчеркнуть, что пока нет наблюдат. эксперим. или теор. оснований считать L отличной от нуля. Во всяком случае, если L?0, то согласно астрофиз. наблюдениям, её абс. величина чрезвычайно мала: |L|<10-55 см-2. Она может играть роль только в космологии и практически не сказывается во всех др. задачах теории Т. Везде в дальнейшем будет положено Л=0.

Внешне ур-ния (9) подобны ур-нию (4) для ньютоновского потенциала. В обоих случаях слева стоят величины, характеризующие поле, а справа — величины, характеризующие материю, создающую поле. Однако ур-ния (9) имеют ряд существ. особенностей. Ур-ние (4) линейно и поэтому удовлетворяет принципу суперпозиции. Оно позволяет вычислить гравитац. потенциал j для любого распределения произвольно движущихся масс. Ньютоновское поле Т. не зависит от движения масс, поэтому ур-ние (4) не определяет их движение. Движение масс определяется из второго закона механики Ньютона (6). В ОТО ур-ния (9) нелинейны, не удовлетворяют принципу суперпозиции. В этой теории нельзя произвольным образом задать правую часть ур-ний (Тik), зависящую от движения материи, а затем вычислить гравитац. поле (gik). Решение ур-ний Эйнштейна приводит к совместному определению движения материи, создающей поле, и к вычислению самого поля. Существенно при этом, что ур-ния поля Т. содержат в себе и ур-ния движения масс в поле Т. С физ. точки зрения это соответствует тому, что в ОТО материя создаёт искривление пространства-времени, к-рое влияет на движение материи, создающей искривление.

В случае слабых гравитац. полей метрика пространства-времени мало отличается от евклидовой, и ур-ния Эйнштейна приближённо переходят в ур-ния (4) и (6) теории Ньютона (если рассматриваются движения, медленные по сравнению с с, и расстояния от источника поля много меньше, чем l=ct, где t — характерное время изменения положения тел в источнике поля). В этом случае можно ограничиться вычислением малых поправок к ур-ниям Ньютона. Эффекты, соответствующие этим поправкам, позволяют экспериментально проверить ОТО (см. ниже). Особенно существенны эффекты теории Эйнштейна в сильных гравитац. полях.

Ряд выводов ОТО качественно отличается от выводов ньютоновской теории Т. Важнейшие из них связаны с возникновением чёрных дыр, сингупярностей пространства-времени (мест, где формально, согласно теории, обрывается существование ч-ц и полей в обычной известной нам форме) и существованием гравитац. волн (гравитационного излучения).

Квантовые эффекты. Ограничения применимости теории тяготения Эйнштейна.

ОТО — неквантовая теория. В этом отношении она подобна классич. электродинамике Максвелла. Однако наиб. общие рассуждения показывают, что гравитац. поле должно подчиняться квант. законам точно так же, как и эл.-магн. поле. В противном случае возникли бы противоречия с принципом неопределённости для эл-нов, фотонов и т. д. Применение квант. теории к гравитации показывает, что гравитац. волны можно рассматривать как поток квантов — гравитонов, представляющих собой нейтр. ч-цы с нулевой массой покоя и со спином 2 (в ед. ћ). В подавляющем большинстве мыслимых процессов во Вселенной и в лаб. условиях квант. эффекты гравитации чрезвычайно слабы, и можно пользоваться неквант. теорией Эйнштейна. Однако квант. эффекты должны стать весьма существенными вблизи сингулярностей поля Т., где искривления пространства-времени очень велики. Из теории размерностей следует, что квант. эффекты в гравитации становятся определяющими, когда радиус кривизны пространства-времени (расстояние, на к-ром проявляются существ. отклонения от геометрии Евклида: чем меньше этот радиус, тем больше кривизна) становится равным величине rпл=?(Gћ/c3). Расстояние rпл наз. планковской длиной; оно ничтожно мало: rпл»10-33 см. В таких условиях ОТО неприменима.

Сингулярные состояния возникают в ходе гравитационного коллапса; сингулярность в прошлом была в расширяющейся Вселенной (см. КОСМОЛОГИЯ). Последовательной квант. теории Т., применимой и для сингулярных состояний, пока не существует. При энергиях ч-ц, соответствующих столь экстремальным состояниям (это энергии ?=?(ћc5/G)»1016 эрг), все виды физ. вз-ствий, по-видимому, проявляются как единое вз-ствие.

Квант. эффекты приводят к рождению ч-ц в поле Т. чёрных дыр. Для чёрных дыр, возникающих из звёзд и имеющих массу, сравнимую с солнечной, эти эффекты ничтожно малы. Однако они могут быть важны для чёрных дыр малой массы (меньше 1015 г), к-рые в принципе могли возникать на ранних этапах расширения Вселенной.

Экспериментальная проверка теории Эйнштейна.

В основе ОТО лежит принцип эквивалентности: все тела независимо от их состава и массы, все виды материи падают в поле Т. с одним и тем же ускорением. Его проверка с возможно большей точностью явл. важнейшей эксперим. задачей. С помощью крутильных весов венг. физик Л. Этвеш доказал справедливость принципа эквивалентности с точностью до 10-8; амер. физик Р. Дикке с сотрудниками довёл точность до 10-10, а В. Б. Брагинский с сотрудниками — до 10-12. Др. проверкой принципа эквивалентности явл. вывод об изменении частоты v света при его распространении в гравитац. поле. Теория предсказывает изменение частоты Dn при распространении между точками с разностью гравитац. потенциалов j1-j2:

Dn/n=(j1-j2)/c2 (10)

Эксперименты в лаборатории подтвердили эту ф-лу с точностью по крайней мере до 1 % (см. МЁССБАУЭРА ЭФФЕКТ), а эксперименты на самолётах и ракетах — до 0,04%.

Кроме этих экспериментов по проверке основ теории, существует ряд опытных проверок её выводов. Теория предсказывает искривление луча света при прохождении вблизи массивных тел. Аналогичное отклонение следует и из ньютоновской теории Т., однако ОТО предсказывает вдвое больший эффект. Многочисл. наблюдения этого эффекта при прохождении света от звёзд вблизи Солнца (во время полных солнечных затмений) подтвердили предсказание ОТО (отклонение на 1,75" у края солнечного диска) с точностью 20%. Гораздо большая точность была достигнута с помощью совр. техники наблюдения внеземных точечных радиоисточников. Этим методом предсказание теории подтверждено с точностью (на 1980) не меньшей 6 %.

Др. эффект, тесно связанный с предыдущим,— большая длительность времени распространения света в поле Т., чем это дают ф-лы без учёта эффектов ОТО. Для луча, проходящего вблизи Солнца, эта дополнит. задержка составляет ок. 2•10-4 с. Эксперименты проводились с помощью радиолокации планет Меркурий и Венера во время их прохождения за диском Солнца, а также с помощью ретрансляции радиолокац. сигналов косм. кораблями. Предсказания теории подтверждены (на 1980) с точностью 2%.

Наконец, ещё одним эффектом явл. предсказываемый ОТО медленный дополнительный (не объясняемый гравитац. возмущениями со стороны др. планет Солнечной системы) поворот в эллиптич. орбите планет, движущихся вокруг Солнца. Наибольшую величину этот эффект имеет для орбиты Меркурия — 43" в столетие. Это предсказание подтверждено экспериментально с точностью до 1%.

Предсказанные ОТО гравитац. волны в прямых экспериментах ещё не открыты, но последствия их излучения системами небесных тел обнаружены. Согласно ОТО, период орбит. движения в двойной звёздной системе должен уменьшаться из-за излучения гравитационных волн. Это уменьшение открыто в системе, одним из компонентов которой является пульсар PSR 193+16. По расчётам ОТО относит. уменьшение периода в этой системе за 1 оборот должно составлять —2,40•10-12, а наблюдения (1982) дают значение (-2,30±0,2) •10-12.

Т. о, все имеющиеся эксперим. данные подтверждают правильность как положений, лежащих в основе теории тяготения Эйнштейна, так и её наблюдат. предсказаний.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ТЯГОТЕНИЕ

(гравитация) - универсальное взаимодействие между любыми видами материи. Если это взаимодействие относительно слабое и тела движутся с нерелятивистскими скоростями, то Т. описывается теорией Ньютона. В случае сильных быстропеременных полей и быстрых движений тел Т. описывается общей теорией относитель ности, созданной А, Эйнштейном, Т. является самым слабым из 4 типов фундам взаимодействий и в квантовой физике- описывается квантовой теорией гравитации, к-рая ещё далека от завершения.

Теория тяготения Ньютона в нерелятивистской классической физике Закон тяготения Ньютона гласит, что две материальные точки с массами т _A и т _В, находящиеся на расстоянии r друг от друга, притягиваются по направлению друг к другу каждая с силой

Коэф. пропорциональности G наз. постоянной тяготения Ньютона или гравитационной постоянной. По совр. данным, G =6,6745(8) •10^-11 м ³/кг•с ². Согласно закону Ньютона, сила Т. зависит только от положения частиц в данный момент времени, и поэтому гравитац. взаимодействие распространяется мгновенно.

В ньютоновской теории справедлив принцип суперпозиции; сила Т., действующая на нек-рую точку А со стороны многих материальных точек, является векторной суммой сил от каждой из них.

При произвольном распределении масс сила Т., действующая в данной точке на любую точечную массу т _А может быть выражена как произведение т _А на вектор g, к-рый наз. напряжённостью поля Т.. в данной точке.

Поле Т.- потенц. поле. Это означает, что его напряжённость может быть выражена как градиент скалярной ф-ции j, наз. гравитац. потенциалом:

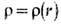Потенциал поля Т. частицы с массой т может быть запи-сан в виде В силу принципа суперпозиции потенциалы полей от разных частиц складываются. Потенциал непрерывного распределения плотности вещества определяется как решение Пуассона уравнения:

где D-Лапласа оператор.

Для изолир. тела или системы тел потенциал определяется, вообще говоря, неоднозначно. Так, напр., к потенциалу можно прибавить произвольную константу.

Ньютонова теория Т. и ньютонова механика явились величайшим достижением естествознания. Они позволяют описать с большой точностью обширный круг явлений, в т. ч, движение естеств. и искусств. тел в Солнечной системе, движения в др. системах небесных тел: в двойных звёздах, в звёздных скоплениях, в галактиках. На основе теории тяготения Ньютона было предсказано существование планеты Нептун и спутника Сириуса и сделаны многие др. предсказания, впоследствии блестяще подтвердившиеся. В совр. астрономии закон тяготения Ньютона является фундаментом, на основе к-рого вычисляются движения и строение небесных тел, их массы, эволюция. Точное определение гравитац. поля Земли позволяет установить распределение масс под её поверхностью (гравиметрия, разведка) и, следовательно, непосредственно решать важные прикладные задачи. Однако в нек-рых случаях, когда поля Т. становятся достаточно сильными, а скорости движения тел в этих полях не малы по сравнению со скоростью света, Т. уже не может быть описано законом Ньютона.

Ограничении применимости теории Ньютона

Теория Ньютона предполагает мгновенное распространение Т. и уже поэтому не может быть согласована со спец. теорией относительности (см. Относительности теория), утверждающей, что никакое взаимодействие не может распространяться со скоростью, превышающей скорость света в вакууме. Нетрудно найти условия, ограничивающие применимость ньютоновой теории Т. Так как эта теория не согласуется со спец. теорией относительности, то её нельзя использовать в тех случаях, когда гравитац. поля настолько сильны, что разгоняют движущиеся в них тела до скорости порядка скорости света с. Скорость, до к-рой разгоняется тело, свободно падающее из бесконечности (предполагается, что там оно имело пренебрежимо малую скорость) до нек-рой точки, равна по порядку величины корню квадратному из модуля гравитац. потенциала j в этой точке (на бесконечности j считается равным нулю). Т. о., теорию Ньютона можно применять только в том случае, если

В полях Т. обычных небесных тел это условие выполняется. Так, на поверхности Солнца а на поверхности белых карликов - порядка 10 ^-3.

Кроме того, ньютонова теория неприменима и к расчёту движения частиц даже в слабом поле Т., удовлетворяющем условию (4), если частицы, пролетающие вблизи массивных тел, уже вдали от этих тел имели скорость, сравнимую со скоростью света. В частности, теория Ньютона неприменима для расчёта траектории света в поле Т. Наконец, теория Ньютона не используется при расчётах переменного поля Т., создаваемого движущимися телами (напр., двойными звёздами) на расстояниях 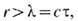где t-характерное время движения в системе (напр., период обращения в системе двойной звезды). Действительно, согласно ньютоновой теории, поле Т. на любом расстоянии от системы определяется положением масс в тот же момент времени, в к-рый определяется поле. Это означает, что при движении тел в системе изменения гравитац. поля, связанные с перемещением тел, мгновенно передаются на любое расстояние r. Но, согласно спец. теории относительности, изменение поля не может распространяться со скоростью, большей с.

Обобщение теории Т. на основе спец. теории относительности было сделано Эйнштейном в 1915-16. Новая теория была названа её творцом общей теорией относительности.

Принцип эквивалентности

Самой важной особенностью поля Т., известной в ньютоновой теории и положенной Эйнштейном в основу его новой теории, является то, что Т. совершенно одинаково действует на разные тела, сообщая им одинаковые ускорения независимо от их массы, хим. состава и др. свойств. Этот факт был установлен опытным путём ещё Г. Галилеем (G. Galilei) и может быть сформулирован как принцип строгой пропорциональности гравитационной, или тяжёлой, массы m_rp, определяющей взаимодействие тела с полем Т. и входящей в закон (1), и инертной массы т _и, определяющей сопротивление тела действующей на него силе и входящей во второй закон механики Ньютона (см. Ньютона законы механики). Действительно, ур-ние движения тела в поле Т. записывается в виде

где a -ускорение, приобретаемое телом под действием напряжённости гравитац. поля g. Если т _гр пропорц. т _и и коэф. пропорциональности одинаков для любых тел, то можно выбрать единицы измерения так, что этот коэф. станет равным единице, 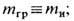тогда они сокращаются в ур-нии (5) и ускорение a не зависит от массы и равно напряжённости g поля Т., a=g в согласии с законом Галилея. (О совр. эксперим. подтверждении этого фундам. факта см. ниже.)

Т. о., тела разной массы и природы движутся в заданном поле Т. совершенно одинаково, если их нач. скорости были одинаковыми. Этот факт показывает глубокую аналогию между движением тел в поле Т. и движением тел в отсутствие Т., но относительно ускоренной системы отсчёта. Так, в отсутствие Т. тела разной массы движутся по инерции прямолинейно и равномерно. Если наблюдать эти тела, напр., из кабины космич. корабля, к-рый движется вне полей Т. с пост. ускорением за счёт работы двигателя, то, естественно, по отношению к кабине все тела будут двигаться с пост. ускорением, равным по величине и противоположным по направлению ускорению корабля. Движение тел будет таким же, как падение с одинаковым ускорением в пост. однородном поле Т. Силы инерции, действующие в космич. корабле, летящем с ускорением, равным ускорению свободного падения на поверхности Земли, неотличимы от сил гравитации, действующих в истинном поле Т. в корабле, стоящем на поверхности Земли. Следовательно, силы инерции в ускоренной системе отсчёта (связанной с космич. кораблём) эквивалентны гравитац. полю. Этот факт выражается п р и н ц и п о м э к в и в ал е н т н о с т и Э й н ш т е й н а. Согласно этому принципу, можно осуществить и процедуру, обратную описанной выше имитации поля Т. ускоренной системой отсчёта, а именно, можно "уничтожить" в данной точке истинное гравитац. поле введением системы отсчёта, движущейся с ускорением свободного падения. Напр., в кабине космич. корабля, свободно (с выключенными двигателями) движущегося вокруг Земли в её поле Т.. наступает состояние невесомости - не проявляются силы Т.

Эйнштейн предположил, что не только механич. движение, но и вообще все физ. процессы в истинном поле Т., с одной стороны, и в ускоренной системе в отсутствие Т., с другой, протекают по одинаковым законам. Этот принцип получил назв. "сильного принципа эквивалентности", в отличие от "слабого принципа эквивалентности", относящегося только к законам механики.

Основная идея теории тяготения Эйнштейна

Рассмотренная выше система отсчёта (космич. корабль с работающим двигателем), движущаяся с пост, ускорением в отсутствие поля Т., имитирует только однородное гравитац. поле, одинаковое по величине и направлению во всём пространстве. Но поля Т., создаваемые отд. телами, не таковы. Для того чтобы имитировать, напр., сферич поле Т. Земли, нужны ускоренные системы с разным направлением ускорения в разл. точках. Наблюдатели в разных системах, установив между собой связь, обнаружат, что они движутся ускоренно относительно друг друга, и тем самым установят присутствие истинного поля Т. Таким образом, истинное поле Т. не сводится просто к введению ускоренной системы отсчёта в обычном пространстве, или, точнее, в пространстве-времени спец. теории относительности. Однако Эйнштейн показал, что если, исходя из принципа эквивалентности, потребовать, чтобы истинное гравитац. поле было эквивалентно локальным соответствующим образом ускоренным в каждой точке системам отсчёта, то в любой конечной области пространство-время окажется искривлённым - неевклидовым. Это означает, что в трёхмерном пространстве геометрия, вообще говоря, будет неевклидовой, а время в разных точках будет течь по-разному. Т. о., согласно теории тяготения Эйнштейна, истинное гравитац. поле является не чем иным, как проявлением искривления (отличия геометрии от евклидовой) четырёхмерного пространства-времени.

В отсутствие Т. движение тела по инерции в пространстве-времени спец. теории относительности изображается прямой линией, или, на матем. языке, экстремальной (геодезич.) линией. Идея Эйнштейна, основанная на принципе эквивалентности и составляющая основу теории Т., заключается в том, что и в поле Т. все тела движутся по геодезич. линиям в пространстве-времени, к-рое, однако, искривлено, и, следовательно, геодезич. линии уже не прямые.

Массы, создающие поле Т., искривляют пространство-время. Тела, к-рые движутся в искривлённом пространстве-времени, в этом случае движутся по одним и тем же геодезич. линиям независимо от массы или состава тела. Наблюдатель воспринимает это движение как движение по искривлённым траекториям в трёхмерном пространстве с переменной скоростью. Но с самого начала в теории Эйнштейна заложено, что искривление траектории, закон изменения скорости - это свойства пространства-времени, свойства геодезич. линий в этом пространстве-времени, а следовательно, ускорение любых тел должно быть одинаково и, значит, отношение тяжёлой массы к инертной [от к-рого зависит ускорение тела в заданном поле Т., ф-ла (5)] одинаково для всех тел и эти массы неотличимы. Т. о., поле Т., по Эйнштейну, есть отклонение свойств пространства-времени от свойств плоского (неискривлённого) многообразия спец. теории относительности.

Вторая важная идея, лежащая в основе теории Эйнштейна.- утверждение, что Т. (т. <е. искривление пространства-времени) определяется не только массой вещества, слагающего тело, но и всеми видами энергии, присутствующими в системе. Согласно этой идее, Т. зависит не только от распределения масс в пространстве, но и от их движения, от давления и натяжений, имеющихся в телах, от эл.-магн. поля и всех др. физ. полей.

Наконец, в теории тяготения Эйнштейна обобщается вывод спец. теории относительности о конечной скорости распространения всех видов взаимодействия. Согласно Эйнштейну, изменения гравитац. поля распространяются в вакууме со скоростью с.

Теория тяготения Эйнштейна

Измерение промежутков времени и пространственных расстояний. В спец. теории относительности в инерциальной системе отсчёта квадрат четырёхмерного "расстояния" в пространстве-времени - интервала ds - между двумя бесконечно близкими событиями записывается в виде

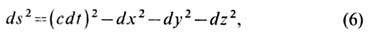
где t - время; х, у, z- прямоуг. декартовы (пространств.) координаты. Эта система координат наз. галилеевой. Выражение (6) не изменяется при Лоренца преобразованиях. Пространство-время, в к-ром можно ввести систему координат так, что в каждой точке ds² записывается в виде (6), наз. псевдоевклидовым, плоским или Минковского пространством-временем. Специальная теория относительности является теорией физ. процессов в таком пространстве.

Если в пространстве-времени Минковского использовать неинерциальные системы отсчёта и недекартовы координаты, то в новых координатах ds² запишется в виде

(m, v = 0, 1, 2, 3), где -произвольные пространств. координаты, x⁰ = ct - временная координата (здесь и далее по одинаковым верх. и ниж. индексам производится суммирование).

В искривлённом пространстве-времени общей теории относительности (в конечных, не малых, областях) уже нельзя ввести декартовы координаты и использование криволинейных координат становится неизбежным. В конечных областях искривлённого пространства-времени ds² записывается в криволинейных координатах в общем виде (7). Зная g_mv как ф-ции 4 координат, можно определить все геом. свойства пространства-времени. Говорят, что величины g_mv определяют метрику пространства-времени, а совокупность всех g_mv наз. м е т р и ч е с к и м т е н з о р о м. С помощью g_mv вычисляются темп течения времени в разных точках системы отсчёта и расстояния между точками в трёхмерном пространстве. Так, ф-ла для вычисления бесконечно малого интервала времени dt по часам, покоящимся в системе отсчёта, имеет вид

Квадрат пространств. расстояния dl² определяется след. образом через пространств. координаты:

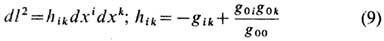
(лат. индексы i, k=1, 2, 3).

Матем. аппаратом, изучающим неевклидову геометрию (см. Риманова геометрия )в произвольных координатах, является тензорное исчисление. Общая теория относительности использует аппарат тензорного исчисления, её законы записываются в произвольных криволинейных координатах (это означает, в частности, запись в произвольных системах отсчёта), как говорят, в ковариантном виде.

Осн. объектами тензорного исчисления являются скаляры, векторы и тензоры разных рангов, к-рые преобразуются по определ. законам при переходе от одной координатной системы к другой (см. Тензор).

Уравнения движения тел и динамические величины

Как уже говорилось, тела в гравитац. поле движутся по геодезич. линиям, если на них не действуют негравитац. силы. Ур-ние геодезич. линии в искривлённом пространстве-времени записывается в виде

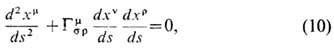
ds измеряется вдоль геодезич. линии. Величины 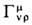наз. с и м в о л а м и К р и с т о ф е л я и выражаются через мет-рич. тензор:

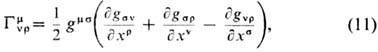
где g^ms определяется из условия 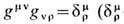-символ Кронекера). В малой окрестности любой точки пространства-времени можно ввести систему координат, движущуюся по инерции, в к-рой метрич. тензор имеет вид (6), а 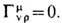Такие системы наз. л о к а л ь н о и н е р ц и а л ь-н ы м и. В этих системах нет никаких гравитац. и инерци-альных сил (свободное падение, невесомость). Если система отсчёта не движется по инерции, то в ней имеется гравитационно-инерциальная сила, определяемая ускорением, к-рое испытывает свободное тело, покоящееся в данном месте в данный момент времени. Вектор ускорения записывается в виде

величина ускорения

Уравнения тяготения Эйнштейна

Осн. задача теории Т.- определение гравитац. поля, что соответствует в теории Эйнштейна нахождению геометрии пространства-времени. Эта последняя задача сводится к нахождению метрич. тензора g_mv.

Ур-ния тяготения Эйнштейна связывают величины g_mv с величинами, характеризующими материю, создающую поле: плотностью, потоками импульса и т. п. Эти ур-ния записываются в виде

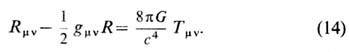
Здесь R_mv -т. <н. тензор Риччи,

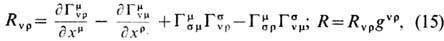
T_mv - тензор энергии-импульса материи. Для газов этот тензор записывается в виде

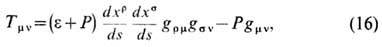
где e=rc² -плотность энергии (включая массу покоя частиц) в системе отсчёта, в к-рой элемент вещества покоится; P- давление. В частном случае, при условии

тензор энергии-импульса можно записать в виде

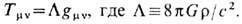
Постоянная L наз. к о с м ол о г и ч е с к о й п о с т о я н н о й. Впервые она была введена в теорию Эйнштейном с целью построить модель Вселенной, к-рая не изменяется с течением времени. Космологич. постоянную можно рассматривать как величину, описывающую плотность энергии и давление (или натяжение) вакуума, или т. н. вакуумоподобного состояния, характеризуемого ур-нием состояния (17). Согласно данным космологии, в сегодняшней Вселенной L либо равна нулю, либо чрезвычайно мала: 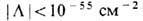Однако, согласно теории ранней Вселенной, в самом начале космологич. расширения, вероятно, L была очень большой, гравитация вакуумоподобного состояния определяла динамику расширения Вселенной (см. Раздувающаяся Вселенная).

Внешне ур-ния (14) подобны ур-нию (3) для ньютонова потенциала. В обоих случаях слева стоят величины, характеризующие поля, а справа - величины, характеризующие материю, создающую поле. Однако ур-ния (14) имеют ряд существ. особенностей. Ур-ние (3) линейно и поэтому удовлетворяет принципу суперпозиции. Оно позволяет вычислить гравитац. потенциал j для любого распределения произвольно движущихся масс. Ньютоново поле Т. не зависит от движения масс, поэтому ур-ние (3) само не определяет непосредственно их движение. Движение масс определяется из второго закона механики Ньютона. Иная ситуация в теории Эйнштейна. Ур-ния (14) нелинейны, не удовлетворяют принципу суперпозиции. В теории Эйнштейна нельзя произвольным образом задать правую часть ур-ний (T_mv), зависящую от движения материи, а затем вычислить гравитац. поле g_mv Решение ур-ний Эйнштейна приводит к совместному определению и движения материи, создающей поле, и к вычислению самого поля. Существенно при этом, что ур-ния поля Т. содержат в себе и ур-ния движения масс в поле Т. С физ. точки зрения это соответствует тому, что в теории Эйнштейна материя создаёт искривление пространства-времени, а это искривление, в свою очередь, влияет на движение материи, создающей искривление. Математически этот факт выражается в том, что ковариантная производная левой части ур-ний Эйнштейна тождественно равна нулю. Из ур-ний (14) тогда следует

(; - знак ковариантного дифференцирования). Ур-ния (18) непосредственно являются ур-ниями движения материи с учётом Т. Так, для случая тензора энергии-импульса (16) в лагранжевых координатах ур-ния (18) переписываются в виде

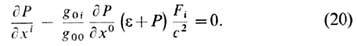
Здесь 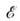-энергия объёма V элемента вещества; 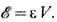Ур-ние (19) описывает изменение энергии за счёт работы сил давления, ур-ние (20) определяет в лагранжевых координатах сохранение импульса вещества. Ур-ния движения тел (10) во внеш. поле Т. также являются следствием ур-ний (18).

В случае слабых гравитац. полей метрика пространства-времени мало отличается от евклидовой и ур-ния Эйнштейна приближённо переходят в ур-ния (3) и (5) теории Ньютона (если рассматриваются движения, медленные по сравнению со скоростью света, и расстояния от источника поля много меньше, чем l=ct где t-характерное время изменения положения тел в источнике поля). В этом случае ньютонов потенциал

В слабых полях можно ограничиться вычислением малых поправок к ур-ниям Ньютона. Эффекты, соответствующие этим поправкам, позволяют экспериментально проверить теорию Эйнштейна (см. ниже). Поле вращающейся массы в теории Эйнштейна отличается от поля невращающейся массы дополнительными, т. <н. г р а в и м а г н и т н ы м и с и л а м и, к-рые действуют на движущиеся тела. Напряжённость гравимагн. поля Н на расстоянии r от массы, имеющей угл. момент g, составляет по порядку величины

Это поле вызывает ускорение тела, движущегося со скоростью, малой по сравнению с с, равное 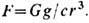Особенно существенны эффекты теории Эйнштейна в сильных гравитац. полях.

Некоторые выводы теории тяготения Эйнштейна

Ряд выводов теории Эйнштейна качественно отличается от выводов ньютоновой теории Т. Важнейшие из них связаны с возникновением чёрных дыр, сингулярностей пространства-времени (мест, где формально, согласно теории, обрывается существование частиц и полей в обычной, известной нам форме) и существованием гравитационных волн.

Черные дыры. Решение ур-ний Эйнштейна (10) в пустоте (T_mv=0) в случае изолированного сферически-симметричного источника поля массой М записывается в виде (решение Шварцшильда)

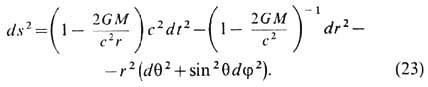
Величина ускорения свободного падения F[см. (13) ] для поля (23) имеет вид

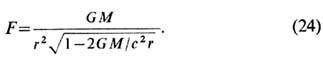
Это выражение отличается от ньютонова корнем в знаменателе. Величина F стремится к бесконечности, когда r стремится к 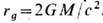. Величина 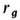наз. гравитационным радиусом. Сфера радиусом 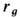наз. сферой Шварцшильда. Вторая космич. скорость в теории Ньютона даётся выражением

Следовательно, при r = r_g , величина V₂ становится равной скорости света. Если сферич. тело массой т сожмётся до размеров, меньших r_g , то свет не сможет выйти из-под сферы Шварцшильда. Такие объекты получили название чёрных дыр. Из чёрных дыр к внеш. наблюдателю не поступает никакой информации.

При сжатии вращающегося тела вывод о возникновении чёрной дыры сохраняется, но поле Т. вокруг неё отличается от выражения (23) наличием гравимагн. сил (см. Чёрные дыры). В этом случае линейные размеры области, из к-рой не может выходить информация (ограничивающая её поверхность наз. г о р и з о н т о м с о б ы т и й), зависят от угл. момента вращающегося сжимающегося тела, но по порядку величины они равны

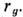
Внутри горизонта событий в чёрной дыре никакие силы не могут удержать тело от дальнейшего сжатия. Процесс сжатия наз. гравитационным коллапсом. При этом растёт поле Т.- увеличивается искривлённость пространства-времени. Доказано, что в результате гравитац. коллапса неизбежно возникает сингулярность пространства-времени, связанная, по-видимому, с возникновением его бесконечной искривлённости. (Об ограничении применимости теории Эйнштейна в таких условиях см. след. раздел.) Теоретич. астрофизика предсказывает возникновение чёрных дыр в конце эволюции массивных звёзд; возможно существование во Вселенной чёрных дыр и др. происхождения. Чёрные дыры, по-видимому, открыты в составе нек-рых двойных звёздных систем.

Гравитационные волны. Теория Эйнштейна предсказывает, что тела, движущиеся с переменным ускорением, будут излучать гравитац. волны. Гравитац. волны являются распространяющимися со скоростью света перем. полями приливных гравитац. сил.

Для слабых гравитац. полей компоненты g_mv мало отличаются от выражений (6). Если представить g_mv как 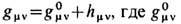имеют вид (6), а 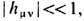то в случае одиночной плоской гравитац. волны, распространяющейся в пустоте вдоль оси х¹, преобразованием координат всегда можно записать решение ур-ния Эйнштейна (14) в виде

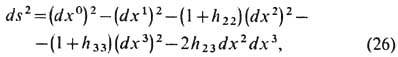
и отличные от нуля компоненты h_mv удовлетворяют соотношениям

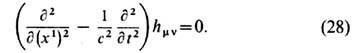
Выражения (26-28) показывают, что гравитац. волны распространяются со скоростью света, поперечны и имеют два независимых состояния поляризации 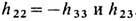Гравитац. волны являются тензорными (в отличие от векторных эл.-магн. волн). В них можно измерять лишь относительные (приливные) ускорения частиц, помещённых в плоскости, перпендикулярной направлению распространения волны. В системе координат (26) не действуют никакие ускорения на частицы, покоящиеся в этой системе (F=0, состояние невесомости), и при прохождении волны меняются лишь относит. расстояния между ними в плоскости ( х² х³).

В каждой точке пространства свободное падение "устраняет" действие гравитац. поля. Следствием этого является невозможность локализовать понятие плотности энергии или плотности потока энергии для гравитац. поля. Однако как глобальные понятия для изолированных систем или в случае гравитац. волн для областей, содержащих много длин волн, понятия энергии и потока энергии вполне определимы. Гравитац. волна, имеющая частоту w и амплитуду 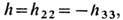обладает плотностью потока энергии (усреднённого по многим длинам волн)

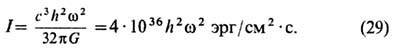
В случае нерелятивистских движений и слабых полей Т. мощность излучения гравитац. волн системами движущихся тел даётся ф-лой

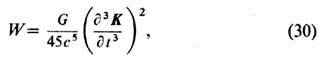
где К- квадрупольный момент источника:

Даже в случае гигантских систем небесных тел излучение гравитац. волн и уносимая ими энергия ничтожны. Так, мощность излучения за счёт движения планет Солнечной системы составляет ок. 10¹¹ эрг/с, что в 10²² раз меньше светового излучения Солнца. Столь же слабо гравитац. волны взаимодействуют с обычной материей. Эксперим. попытки обнаружить, зарегистрировать гравитац. волны пока (1996) оказались неудачными.

Квантовые эффекты. Ограничения применимости теории тяготения Эйнштейна

Теория Эйнштейна-неквантовая теория. В этом отношении она подобна классич. электродинамике Максвелла. Однако наиб. общие рассуждения показывают, что гравитац. поле должно подчиняться квантовым законам точно так же, как и эл.-магн. поле. В противном случае возникли бы противоречия с принципом неопределённости для электронов, фотонов и т. д. Применение квантовой теории к гравитации показывает, что гравитац. волны можно рассматривать как поток квантов - гравитонов. Гравитоны представляют собой нейтральные частицы с нулевой массой покоя и со спином 2 (в единицах ).

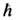В подавляющем большинстве мыслимых процессов во Вселенной и в лаб. условиях квантовые эффекты гравитации чрезвычайно слабы, и можно пользоваться неквантовой теорией Эйнштейна. Однако квантовые эффекты должны стать весьма существенными вблизи сингулярно-стей поля Т., где искривления пространства-времени очень велики. Теория размерностей указывает, что квантовые эффекты в гравитации становятся определяющими, когда радиус кривизны пространства-времени (расстояние, на к-ром проявляются существенные отклонения от геометрии Евклида: чем меньше этот радиус, тем больше кривизна) становится равным величине Расстояние r _Пл наз. п л а н к о в с к о й д л и н о й; оно ничтожно мало: 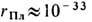см. В таких условиях теория тяготения Эйнштейна неприменима.

Сингулярные состояния возникают в ходе гравитац. коллапса; сингулярность в прошлом была в расширяющейся Вселенной (см. Космология). Последоват. квантовой теории Т., применимой и в сингулярных состояниях, пока не существует. О совр. состоянии исследований квантовых эффектов в Т., включая проблемы супергравитации, многомерных единых теорий поля, суперструн и др., см. в статьях Квантовая теория гравитации и Гравитационное взаимодействие.

Квантовые эффекты приводят к рождению частиц в поле Т. чёрных дыр. Темп излучения частиц определяется массой М (а значит, размером) чёрной дыры и приблизительно соответствует излучению тела, нагретого до темп-ры

Полная мощность излучения составляет по порядку величины

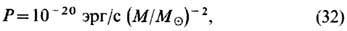
где 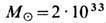г - масса Солнца. Для чёрных дыр, возникающих из звёзд и имеющих массу, сравнимую с солнечной, эти эффекты пренебрежимо малы. Так, для чёрной дыры с М=10 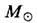имеем 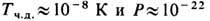эрг/с. Однако они могут быть важны для чёрных дыр малой массы (<10¹⁵ г), к-рые в принципе могли возникать на ранних этапах расширения Вселенной.

Экспериментальная проверка теории Эйнштейна. Другие теории тяготения

Поскольку в основе теории тяготения Эйнштейна лежит принцип эквивалентности, его проверка с возможно большей точностью является важнейшей эксперим. задачей. Л. Этвеш (L. Eotvos) с помощью крутильных весов доказал справедливость принципа эквивалентности с точностью до 10^-8, Р. Дикке (R. Dicke) с сотрудниками довёл точность до 10^-10, а В. Б. Брагинский с сотрудниками - до 10^-12.

Другой проверкой принципа эквивалентности является проверка вывода об изменении частоты v света при его распространении в гравитац. поле. Теория предсказывает изменение частоты Dv (см. Красное смещение )при распространении между точками с разностью гравитац. потенциалов

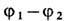
Эксперименты в лаборатории подтвердили эту ф-лу с точностью по крайней мере до 1% (см. Мёссбауэра эффект), а с помощью водородного мазера, установленного на ракете, точность доведена до 2 · 10 ^-4 предсказываемой величины (1980). В теории Эйнштейна постоянная Т. не меняется с течением времени. Справедливость этого факта проверялась путём радарных наблюдений движения планет Меркурия и Венеры, движения космич. кораблей, измерений движения Луны с помощью лазера, а также наблюдений движения нейтронной звезды - пульсара PSR 1913+16, входящей в состав двойной звёздной системы.

Наблюдения подтверждают неизменность G с точностью

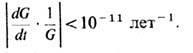
Кроме этих экспериментов по проверке основ теории существует ряд опытных проверок её выводов. Теория предсказывает искривление луча света при прохождении вблизи тяжёлой массы. Аналогичное отклонение следует и из ньютоновой теории Т., однако теория Эйнштейна предсказывает вдвое больший эффект. Многочисл, наблюдения этого эффекта при прохождении света от звёзд вблизи Солнца (во время полных солнечных затмений) подтвердили предсказание теории Эйнштейна (отклонение на 1,75 " у края солнечного диска) с точностью ~11%. Гораздо большая точность была достигнута с помощью совр. техники наблюдения внеземных точечных радиоисточников. Этим методом предсказание теории подтверждено с точностью (по данным 1984) ок. 0,3%.

Другим эффектом, тесно связанным с предыдущим, является большая длительность времени распространения света в поле Т., чем это дают ф-лы без учёта эффектов теории Эйнштейна. Для луча, проходящего вблизи Солнца, эта дополнит. задержка составляет ок. 2•10^-4 с. Эксперименты проводились с помощью радиолокации планет Меркурий и Венера во время их прохождения за диском Солнца, а также с помощью ретрансляции радиолокац. сигналов космич. кораблями, в т. ч. кораблями, движущимися вокруг планеты Марс. Предсказание теории подтверждены (по данным 1979) с точностью 0,1%.

Наконец, ещё одним эффектом является предсказываемый теорией Эйнштейна медленный дополнительный (не объясняемый гравитац. возмущениями со стороны др. планет Солнечной системы) поворот эллиптич. орбит планет, движущихся вокруг Солнца. Наиб. величину этот эффект имеет для орбиты Меркурия-43 " в столетие. По совр. данным это предсказание подтверждено экспериментально с точностью до 0,5%. На точность проверки этого эффекта влияет неопределённость знания величины квадрупольно-го момента Солнца. Согласно стандартной модели, квадрупольный момент Солнца мал и его вклад в поворот орбиты Меркурия на 3-4 порядка меньше, чем предсказываемый теорией Эйнштейна. Однако нек-рые наблюдат. данные указывают на возможность того, что квадруполь-ный момент Солнца значителен и его влияние на поворот орбиты Меркурия сравнимо с предсказаниями теории Эйнштейна. Наблюдения, определяющие квадрупольный момент Солнца, очень трудны, и вопрос о его величине до сих пор остаётся открытым.

Эффекты теории Эйнштейна должны быть весьма значительными при движении звёзд в тесных двойных системах. Проверка этих эффектов с наиб. точностью возможна при изучении движения пульсара PSR 1913 + 16 в двойной системе. Здесь поворот оpбиты за счёт эффектов теории Эйнштейна составляет 4,2^o в год, и за 14 лет наблюдений (1975-89) поворот составил почти 60^o. Наблюдения этого пульсара впервые подтвердили предсказываемую теорией Эйнштейна потерю энергии двойной системой за счёт излучения гравитац. волн. Вследствие этого эффекта должен уменьшаться со временем период обращения звёзд. Наблюдения подтверждают предсказание с точностью до 1 %.

Т. о., все имеющиеся эксперим. данные подтверждают правильность как положений, лежащих в основе теории тяготения Эйнштейна, так и её наблюдат. предсказаний. Следует отметить, что пока эксперим. данные относятся почти исключительно к сравнительно слабым полям Т. с 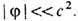Неоднократно делались попытки построить теорию Т., обобщающую теорию Ньютона на случай сильных полей, но отличную от общей теории относительности. В нек-рых из этих теорий все поправки к ньютоновой теории, к-рые проверены экспериментально, совпадают с поправками, предсказываемыми теорией Эйнштейна, и, т. о., эти данные ещё не указывают однозначно на безусловную справедливость общей теории относительности. Попытки построения др. теорий Т. выявили ряд важных особенностей теории Эйнштейна. Существуют альтернативные формулировки этой теории, напр, т. н. полевая формулировка [7]. Нек-рых авторов не удовлетворяет подход к проблеме энергии в общей теории относительности, отличный от подхода в полевых теориях, и поэтому предлагается др. теория Т. (см., напр., [10], [11 ]).

На протяжении более 80 лет теория Эйнштейна демонстрирует свою необычайную стройность, экономность построения, красоту. Все её предсказания подтверждаются, и нет ни одного факта, противоречащего ей. Более того, вероятное открытие астрофизиками чёрных дыр продемонстрирует справедливость предсказаний теории и в области сильных полей Т.

Лит.;1) Эйнштейн А., Собрание научных трудов, т. 1-4, М., 1965-67; 2) Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; 3) Мизнер Ч., Торн К., Уилер Дж., Гравитация, пер. с англ., т. 1-3, М., 1977; 4) Зельдович Я. Б., Новиков И. Д., Теория тяготения и эволюция звезд, М., 1971; 5) Брумберг В. А., Релятивистская небесная механика, М., 1972; 6) Новиков И. Д., Фролов В. П., Физика черных дыр, М., 1986; 7) Грищук Л. П., Петров А. <Н., Гамильтоново описание гравитационного поля и калибровочные симметрии, "ЖЭТФ", 1987, т. 92, с. 9; 8) Грищук Л, П., Гравитационно-волновая астрономия, "УФН", 1988, т. 156, в. 2, с. 297; 9) Will С., Experimental gravitation, from Newton's principles to Einstein's general relativity, в кн.: Three hundred years of gravitation, Camb., 1987, p. 80; 10) Логунов А. А., Мест-виришвили М. А., Основы релятивистской теории гравитации, 2 изд., М., 1986; 11) Зельдович Я. Б., Грищук Л. П., Тяготение, общая теория относительности и альтернативные теории. "УФН", 1986, т. 149, в. 4, с. 695. И. Д. Новиков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.