РЕЗОНАНС

РЕЗОНАНС

       

(франц. resonance, от лат. resono — звучу в ответ, откликаюсь), относительно большой селективный (избирательный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте её собств. колебаний. При Р. происходит резкое возрастание амплитуды вынужденных колебаний осциллятора. Р. как механич. и акустич. явление впервые описан итал. учёным Г. Галилеем, а в эл.-магн. системах — на примере колебательного контура—англ. учёным Дж. Максвеллом (1868). Различают Р., возникающий в результате воздействия внеш. периодич. силы на осциллятор, и параметрич. Р., возникающий вследствие периодич. изменения одного из энергоёмких параметров осциллятора. Данная статья посвящена первому случаю Р.; о параметрич. Р. (см. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС).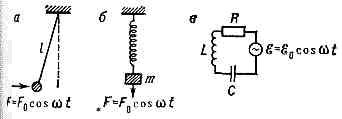

Рис. 1. Пример гармонич. осцилляторов: а— маятник; б— масса на пружине; в — колебательный контур.

Р. линейных систем. В простейшем случае Р. наступает, когда внеш. периодич. сила F изменяется с частотой со, равной частоте w0 собств. колебаний системы (w=w0). В ходе раскачки осциллятора (напр., груза с массой m, подвешенного на нити или пружине,— рис. 1, а, б) его скорость v направлена в ту же сторону, что и сила F, поэтому он получает за период приращение энергии, пропорциональное размаху колебаний. В результате размах колебаний изменяется от периода к периоду в арифметич. прогрессии — линейно (рис. 2, а).

Однако в реальных условиях всегда существуют факторы, ограничивающие амплитуду колебаний и определяющие возможность существования Р. Это прежде всего диссипация энергии (трение) в системе и неточное совпадение вынуждающей силы с собств. частотой осциллятора (т. н. расстройка частоты).

Рис. 2. Нарастание колебаний при w®w0: а — неограниченное; б — при наличии диссипации энергии.

При точном соблюдении условия w=w0 раскачка осциллятора ограничивается диссипацией энергии (рис. 2, б). Колебания нарастают до тех пор, пока внеш. сила не уравновесится силой трения Fтр=-gv (где g — постоянный коэфф.). Если же частота внеш. силы несколько отличается от собств. частоты осциллятора (существует расстройка Р.), то даже при отсутствии трения колебания нарастают лишь до тех пор, пока фазовый сдвиг Dj между скоростью осциллятора и внеш. силой не возрастёт до я/2. Амплитуда вынужденных колебаний в этом случае будет определяться расстройкой Р., т. е. величиной w-w0. Т. о., Р. возможен, когда между внеш. силой и вынужденными колебаниями устанавливаются такие фазовые соотношения, при к-рых в систему поступает наибольшая мощность, т. к. скорость системы оказывается в фазе с внеш. силой.

Колебания осциллятора под действием периодич. силы F=F0coswt в общем случае при наличии диссипации энергии и расстройки можно описать дифф. ур-нием: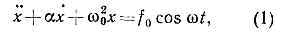

где в случае маятника (рис. 1, а) w20=g/l, a=g/m, f0=F0/m,

l — длина подвеса, g — ускорение силы тяжести; для колебат. контура, возбуждаемого электродвижущей силой ?=?0coswt (рис. 1, в), w20=1lLc, a=R/L, f0=?0/L.

Решение ур-ния (1), описывающее установившиеся вынужденные колебания, имеет вид:

x=x0cos(wt+j), где tgj=aw/(w20-w2),

а стационарная амплитуда этих колебаний

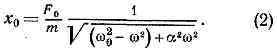Зависимость амплитуды колебаний x0 от частоты внеш. силы w (рис. 3) наз. р е з о н а н с н о й к р и в о й. Ширина этой кривой (т. н. ширина линии Р.) Dw представляет собой интервал расстроек Р., внутри к-рого x20 отличается от макс. значения не больше, чем вдвое. Ширина линии Р. тем уже, чем больше добротность осциллятора Q=w/a, поскольку Dw=w0/Q.

Рис. 3. a — резонансные кривые линейных осцилляторов при разл. добротности Q (Q3>Q2>Q1); б — зависимость фазы j от частоты при резонансе.

Р. нелинейных систем. При большой амплитуде колебаний осциллятор становится нелинейным, его собств. колебания несинусоидальны, а частота собств. колебаний w0 зависит от их амплитуды x0.

Рис. 4. Резонансная кривая нелинейного осциллятора (схематически) в зависимости от амплитуды внеш. силы: а — при малой, б — при умеренной, в — при большой; штрих-пунктиром дана связь между размахом колебаний x0 и собств. частотой осциллятора w0; пунктиром — неустойчивое значение амплитуды колебаний осциллятора; стрелки — изменение амплитуды при перестройке частоты.

Вследствие этого Р. нелинейного осциллятора отличается тем, что в ходе его раскачки внеш. силой расстройка Р. изменяется. Если это изменение больше ширины линии Р. Dw (при достаточно большой амплитуде силы; рис. 4), то, чтобы избежать выхода из Р., необходимо подстраивать частоту со внеш. силы вслед за частотой осциллятора w0(x0). Макс. амплитуда, к-рую таким образом можно придать осциллятору, определяется, как и для линейных осцилляторов, балансом между диссипацией энергии и её поступлением от источника внеш. силы. Зависимость стационарной амплитуды осциллятора от частоты может оказываться в этом случае неоднозначной (верхняя кривая на рис. 4); при перестройке частоты внеш. силы имеют место скачкообразные изменения амплитуды колебании осциллятора, а конкретное значение амплитуды в области неоднозначности зависит от того, в какой последовательности перестраивалась частота силы при раскачке осциллятора (имеет место гистерезис).

Особую группу нелинейных колебат. систем составляют системы, в к-рых происходит компенсация диссипативных потерь благодаря притоку энергии от внеш. постоянного источника. В таких системах устанавливаются незатухающие колебания с вполне определёнными амплитудой и частотой автоколебания. Внешняя периодич. сила малой амплитуды не может существенно повлиять на амплитуду автоколебаний, но может «навязать» генератору свою частоту w, если последняя принадлежит узкому интервалу частот, включающему частоту автоколебаний w0; этот интервал тем больше, чем больше амплитуда внешней силы. Это резонансное явление наз. синхронизацией колебаний.

Р. может наступить не только при совпадении частоты внеш. воздействия с частотой собств. колебаний осциллятора, но и при кратном или дробном соотношении частот (т. н. комбинац. P.): pw=qw0, где р и q — любые целые положит. числа. В простейшем случае р и q — это номера обертонов (гармоник), представленных соответственно во внеш. силе и в собств. колебаниях осциллятора.

Р. в системах с неск. степенями свободы. В системах с числом степеней свободы n?2 и в распределённых системах Р. сохраняет все осн. черты Р. в системе с одной степенью свободы. В линейном приближении собств. колебания этих систем представляют собой набор нормальных колебаний (мод). Если отклик системы представляет собой суммарный отклик всех степеней свободы, резонансная кривая будет наложением резонансных кривых отд. норм. колебаний и может иметь сложный характер. Так, в системе с двумя степенями свободы, ввиду того что собств. колебания могут происходить с двумя разл. частотами, Р. наступает при совпадении частоты гармонич. внеш. воздействия как с одной, так и с другой норм. частотой системы (рис. 5). Подбором параметров норм. колебаний можно создать резонансную кривую практически любой формы, что широко используется, напр. в радиотехнике, для создания фильтров частот.

Рис. 5. Резонансная кривая колебат. системы с двумя степенями свободы при сильно разнесённых (a) и при близких друг к другу (б) частотах норм. колебаний w1 и w2.

Для резонансного возбуждения к.-л. моды в системе с большим числом степеней свободы необходимо не только обеспечить резонансное соотношение между частотой этой моды и частотой внеш. силы, но и создать такие условия, чтобы воздействие силы на разные элементы системы не оказалось взаимно скомпенсированным (чтобы внеш. сила не была ортогональна норм. колебанию). Напр., при воздействии на струну в точке, где находится узел данного норм. колебания, резонансное возбуждение струны не происходит, т. к. внеш. сила, приложенная к неподвижной точке струны, работы не совершает, колебание струны не возникает и Р. не наблюдается. Резонансные взаимодействия. В системах с мн. степенями свободы явления резонансного характера могут происходить не только вследствие внеш. воздействия, но и в процессе собств. колебаний системы. Напр., в системе, представляющей собой две слабовзаимодействующие колебат. подсистемы с близкими частотами, может происходить резонансная перекачка энергии из одной подсистемы в другую. В др. случаях моды системы, независимые при малой амплитуде колебаний, с ростом амплитуды могут начать взаимодействовать (обмениваясь энергией) из-за нелинейности системы, если частоты мод wi (i=1, 2, 3, ...) удовлетворяют комбинац. резонансным условиям типа рw1=qw2 или рw1=qw2+rw3 (р, q, r=1, 2, 3, ...).

Согласно законам квантовой механики, энергия атомов и молекул может принимать дискретные значения. Совокупность этих значений энергии ?i — энергетич. спектр — определяет спектр частот системы wij=(?i-?j)/ћ, где i и j — номера энергетических уровней. При совпадении частоты внешнего воздействия (обычно эл.-магн. поля) с одной из частот wij возможен Р. Примерами таких резонансных вз-ствий могут служить электронный парамагнитный резонанс, ядерный магнитный резонанс, ферромагнитный резонанс и др. Резонансные спектры атомов, молекул и их соединений служат основой спектроскопич. анализа самых разнообразных в-в (см. СПЕКТРОСКОПИЯ). Резонансный отбор энергии у систем возбуждённых осцилляторов (атомов, молекул, эл-нов, колеблющихся в магн. поле, и т. п.) с помощью перем. эл.-магн. полей — основа действия генераторов когерентного эл.-магн. излучения — мазеров и лазеров. Р. играет большую роль в природе, науке и технике. Р. сооружений и машин при периодич. внешних воздействиях может явиться причиной катастроф. Чтобы избежать резонансного воздействия, подбирают соответствующим образом свойства системы или используют успокоители колебаний, основанные на явлении антирезонанса. В радиотехнике благодаря Р. можно отделить сигналы одной (нужной) радио- или телестанции от всех других.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

РЕЗОНАНС

(франц. resonance, от лат. resono - откликаюсь) - частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин "Р." относится лишь к случаю силового воздействия.

Резонанс в линейных системах с одной степенью свободы. Пример простейшего случая Р. представляют вынужденные колебания, возбуждаемые сторонним источником - гармонической эдс ~ E₀cospt с амплитудой Е ₀ и частотой p - в колебательном контуре (рис. 1, а).

Рис. 1. Колебательные системы с одной степенью свободы: последовательный ( а) и параллельный ( б) колебательные контуры, математический маятник ( в) и упругий осциллятор ( г),

Амплитуда x и фаза f вынужденных колебаний заряда [q(t) = xcos(pt+f)] определяются амплитудой и частотой внеш. силы:

где F= E₀/L,d = (R + R_i)/2L.

Зависимость амплитуды х стационарных вынужденных колебаний от частоты p вынуждающей силы при постоянной её амплитуде наз. резонансной кривой (рис. 2). В линейном колебат. контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы.

Вложение энергии в колебат. контур пропорц. первой степени, а диссипация энергии пропорц. квадрату амплитуды колебаний. Это обеспечивает ограничение амплитуд стационарных вынужденных колебаний при Р. Приближение частоты p к собств. частоте w₀ сопровождается ростом амплитуды вынужденных колебаний, тем более резким, чем меньше коэф. затухания d. При Р. ток, протекающий через контур, I == = pxcos(pt + f - p/2), находится в фазе с эдс сторон него источника (f = p/2). Уменьшение амплитуды вынужденных колебаний при неточной настройке обусловлено нарушением синфаз-ности тока и напряжения в цепи.

Важной характеристикой резонансных свойств колебат. системы (осциллятора) является добротность Q, к-рая, по определению, равна умноженному на 2p отношению энергии, запасённой в системе, к энергии, рассеиваемой за период колебаний. При воздействии на резонансной частоте амплитуда вынужденных колебаний x в Q раз больше, чем в квазистатич. случае, при Число периодов колебаний, в течение к-рых происходит установление стационарной амплитуды, также пропорц. Q. Наконец, добротность определяет частотную избирательность резонансных систем. Ширина полосы Р. Dw, в пределах к-рой амплитуда вынужденных колебаний спадает в раз от х, обратно пропорц. добротности: Dw = w₀/Q = 2d.

При Р. в электрич. цепях реактивная часть комплексного импеданса обращается в нуль. При этом в после-доват. цепи падения напряжения на катушке индуктивности и на конденсаторе имеют амплитуду QE₀. Однако они складываются в противофазе и взаимно компенсируют друг друга. В параллельной цепи (рис. 1, б )при Р. происходит взаимная компенсация токов в ёмкостной и индуктивной ветвях. В отличие от последоват. Р., при к-ром внеш. силовое воздействие осуществляется источником напряжения, в параллельном контуре резонансные явления реализуются только в том случае, когда внеш. воздействие задаётся источником тока. Соответственно Р. в последоват. контуре называют Р. напряжений, а в параллельном контуре - Р. токов. Если в параллельный контур вместо генератора тока включить генератор напряжения, то на резонансной частоте будут выполняться условия не максимума, а минимума тока, поскольку вследствие компенсации токов в ветвях, содержащих реактивные элементы, проводимость цепи оказывается минимальной (явление антирезонанса).

Подобными чертами обладает явление Р. в механич. и др. колебат. системах. В линейных системах, согласно принципу суперпозиции, реакцию системы на периодич. несинусоидальное воздействие можно найти как сумму откликов на каждую из гармонич. компонент воздействия. Если период несинусоидальной силы равен Т, то резонансное возрастание колебаний может происходить не только при условии w₀ ! 2p/Т, но в зависимости от формы E(t )и при условиях w₀ ! 2pn/T, где n =1, 2,... (Р. на гармониках).

Резонансные кривые определяют, наблюдая изменение амплитуды вынужденных колебаний либо при медленной перестройке частоты p вынуждающей силы, либо при медленном изменении собств. частоты w₀. При высокой добротности осциллятора (Q1) оба способа дают практически одинаковые результаты. Частотные характеристики, полученные при конечной скорости изменения частоты, отличаются от статич. резонансных кривых, соответствующих бесконечно медленной перестройке: на динамич. частотных характеристиках наблюдается смещение максимума в направлении перестройки частоты, пропорц. m, где - время релаксации колебаний в контуре,

Рис. 3. Статические и динамические амплитудно-частотные характеристики резонанса при различных скоростях нарастания частоты: p(t)= w₀ + t/m, m = 0(1),0,0625 (г), 0,25(3), 0,695 (4).

t*- время, в течение к-poгo частота p находится в пределах полосы резонанса Dw. При быстрой перестройке частоты, по мере роста m, происходит уменьшение высоты и расширение резонансных кривых, причём их форма становится более асимметричной (рис. 3).

Резонанс в линейных колебательных системах с несколькими степенями свободы. Колебат. системы с неск. степенями свободы представляют собой совокупность взаимодействующих осцилляторов. Примером может служить пара колебат. контуров, связанных за счёт взаимной индукции (рис. 4). Вынужденные колебания в такой системе описываются ур-ниями

Индуктивная связь приводит к тому, что колебания в отд. контурах не могут происходить независимо друг от друга. Однако для любой колебат. системы с неск. степенями свободы можно найти нормальные координаты, к-рые являются линейными комбинациями независимых переменных. Для нормальных координат система ур-ний, подобная (2), преобразуется в цепочку ур-ний для вынужденных колебаний такого же вида, как для одиночных колебат. контуров, с тем отличием, что воздействие на каждую из нормальных координат оказывают силы, приложенные, вообще говоря, в разных частях совокупной колебат. системы. При рассмотрении законов движения в нормальных координатах справедливы все закономерности Р. в системах с одной степенью свободы.

Рис. 4. Колебательная система с двумя степенями свободы - пара контуров со связью за счёт взаимоиндукции.

Резонансное нарастание колебаний происходит во всех частях колебат. системы на одних и тех же частотах (рис. 5), равных частотам собств. колебаний системы. Нормальные частоты не совпадают с парциальными, т. е. с собств. частотами осцилляторов, входящих в совокупную систему. Если частота сторонней силы равна одной из парциальных частот, то в совокупной системе Р. не наступает. Напротив, в этом случае амплитуды вынужденных колебаний достигают минимума, аналогично случаю антирезонанса в системе с одной степенью свободы. Возможность подавления колебаний, частота к-рых равна одной из парциальных, используется в электрич. фильтрах и успокоителях механич. колебаний.

В системе, состоящей из слабо связанных осцилляторов с одинаковыми парциальными частотами, резонансные максимумы, отвечающие близким нормальным частотам, могут сливаться, так что частотная характеристика имеет один максимум (рис. 6). Увеличение связи между осцилляторами приводит к росту интервала между нормальными частотами системы. Изменение формы резонансных кривых при увеличении коэф. связи иллюстрирует рис. 6. Система осцилляторов при связи, близкой к критической, имеет частотную характеристику, уплощённую вблизи Р., причём крутизна её склонов выше, чем у одиночного осциллятора с таким же уровнем потерь. Это свойство обычно используется для создания полосовых электрич. фильтров.

Рис. 6. Резонансные кривые двухконтурной колебательной системы при gQ = 1(1), и 2(3); g = M/L, L₁ = L₂.

Резонанс в распределённых колебательных системах. В распределённых системах (см. Система с распределёнными параметрами )амплитуда и фаза колебаний зависят от пространственных координат. Линейные распределённые колебат. системы характеризуются набором нормальных частот и собств. ф-ций, к-рые описывают пространственное распределение амплитуд собств. колебаний. Резонансные свойства (добротность) распределённых систем определяются не только собств. затуханием, но и связью с окружающей средой, в к-рую происходит излучение части энергии колебаний (электрич., упругих и др.). В распределённых системах, обладающих высокой добротностью (Q1), вынужденные колебания представляют собой стоячие волны, пространственное распределение амплитуд к-рых является суперпозицией собств. ф-ций (мод), а фаза колебаний одинакова во всех точках. Действие сторонних сил с частотами, близкими к собственным, ведёт к резонансному нарастанию амплитуды вынужденных колебаний во всех точках объёма распределённой резонансной системы (резонатора).

В распределённых системах сохраняют силу все общие свойства Р. Особенностью Р. в распределённых системах (равно как и в системах с неск. степенями свободы) является зависимость амплитуд вынужденных колебаний не только от частоты, но и от пространственного распределения вынуждающей силы. Р. наступает, если пространственное распределение внеш. силы повторяет форму собств. ф-ции, а частота равна соответствующей нормальной частоте. При неблагоприятном пространственном распределении сторонней силы вынужденные колебания не возбуждаются. Это происходит, в частности, тогда, когда сосредоточенная сила прикладывается в точках, для к-рых амплитуда соответствующего нормального колебания обращается в нуль. Так, прикладывая сосредоточенную силу в точке, являющейся узловой для перемещений струны, невозможно возбудить её колебания, поскольку работа силы будет равна нулю. Если распределение сил таково, что работа, совершаемая ими в разл. частях системы, имеет противоположные знаки и в целом не приводит к изменению энергии, вынужденные колебания также не возбуждаются.

Резонанс в нелинейных колебательных системах. В упругих системах нелинейным элементом является пружина, для к-рой связь между деформацией и упругой силой нелинейна, т. е. нарушается закон Гука. В электрич. системах примером нелинейного диссипа-тивного элемента является диод, вольт-амперная характеристика к-рого не подчиняется закону Ома. Нелинейными реактивными (энергоёмкими) элементами являются конденсаторы с сегнетоэлектриком или катушки индуктивности с ферритовыми сердечниками. Параметры этих элементов - ёмкость, индуктивность, сопротивление, а также собств. частоту и коэф. затухания в нелинейных системах можно считать ф-циями тока или напряжения. При этом в нелинейных системах не выполняется суперпозиции принцип.

В нелинейных системах гармонич. сила возбуждает негармонич. колебания, в спектре к-рых имеются кратные частоты, поэтому Р. на гармониках происходит p при синусоидальной внеш. силе. В колебат. системах, обладающих достаточно высокой добротностью и частотной избирательностью, наиб. амплитуду имеет та спектральная компонента, частота к-рой близка к частоте Р. Рассматривая лишь колебания с частотой, близкой к резонансной, можно и в этом случае получить семейство резонансных кривых. Для системы с нелинейными реактивными (энергоёмкими) элементами при r ! w₀ эти кривые изображены на рис. 7. Форма резонансной кривой зависит от амплитуды вынуждающей силы и по мере её увеличения становится всё более асимметричной. Поскольку частота собств. колебаний нелинейного осциллятора зависит от их амплитуды, то и максимумы на резонансных кривых сдвигаются в сторону более высоких или более низких частот. Начиная с нек-рого значения амплитуды силы, резонансные кривые приобретают неоднозначную клювообразную форму. В определённом интервале частот стационарная амплитуда вынужденных колебаний оказывается зависящей от предыстории установления колебаний (явление колебат. гистерезиса). При этом части резонансных кривых, соответствующих неустойчивым состояниям, образуют на плоскости ( х, р )область физически нереализуемых режимов (на рис. 7 заштрихована).

Рис. 7. Семейство амплитудно-частотных кривых в случае нелинейного резонанса при различных амплитудах сторонней силы (F₁ < F₂< < F₃.< F₄). Пунктир - неустойчивый участок резонансной кривой. Заштрихована область неустойчивых состояний. Стрелками отмечены точки скачкообразного изменения амплитуд колебаний при перестройке частоты вверх ( АВ) и вниз (CD).

На явление нелинейного Р. в распространённых колебат. системах могут оказать существ. влияние эффекты самофокусирования и образования ударных волн, особенно в тех случаях, когда на длине резонатора укладывается большое число волн.

Явления, родственные резонансу. В нелинейных колебат. системах внеш. периодич. воздействие вызывает не только возбуждение вынужденных колебаний, но и модуляцию энергоёмких и диссипативных параметров. Явление возбуждения колебаний при периодич. модуляции энергоёмких параметров наз. па-раметрич. резонансом.

Если глубина модуляции энергоёмкого параметра недостаточна для возбуждения параметрич. Р., в колебат. системе происходит частичное восполнение потерь. Резонансный отклик на действие слабого сигнала с частотой р ! w₀ при этом такой же, как у линейного осциллятора с более высокой добротностью. Кроме того, образуются колебания комбинац. частот mр + nw _М, где w _М - частота модуляции параметра, При совпадении частоты р и (w _М - р) вынужденные колебания в параметрически регенерированной системе зависят от соотношений между фазами параметрич. воздействия и слабой силы (сигнала). При этом может происходить как увеличение, так и уменьшение амплитуды вынужденных колебаний по сравнению с отсутствием параметрич. регенерации (явления "сильного", и "слабого" Р.).

Эффект регенерации потерь и повышения эквивалентной добротности имеют место в резонансных системах с нелинейными потерями, к-рые содержат элементы С отрицательным дифференциальным сопротивлением пли цепи положительной обратной связи. Такие системы наз. потенциально автоколебательными. Если на потенциально автоколебат. систему воздействует пе-рподич. сила значит. амплитуды с частотой р, она может влиять на затухание колебаний в системе так, что в течение определённой доли периода действия силы затухания оно становится отрицательным. В результате в потенциально автоколебат. системе возбуждаются колебания на частоте w, близкой к собственной, если дополнительно выполнено условие w = р/n. Случай n = 1 отвечает синхронизации частоты автоколебаний внеш. силой. При n2 данное явление носит назв. автопараметрич. возбуждения, по аналогии с параметрическим резонансом, в отличие от к-рого при автопараметрич. возбуждении происходит модуляция не энергоёмких, а диссипативных параметров системы.

Термин "Р." употребляется и по отношению к процессам в квантовых системах, когда частота внеш. воздействия (излучения) равна частоте квантового перехода, так что выполняется условие

где - энергия соответственно n -, m - го уровней квантовой системы. При выполнении (3) резко возрастают вероятности квантовых переходов, что проявляется как увеличение интенсивности обмена энергией - поглощения и излучения (см. Квантовая электроника, Лазер).

Р. может быть причиной неустойчивости и разрушений механич. инженерных конструкций и электрич. сетей. В вибропреобразователях Р. позволяет достигать значит. амплитуд упругих колебаний благодаря периодич. действию сравнительно слабой силы. В радиофизике и радиотехнике явление Р. лежит в основе мн. способов фильтрации сигналов разных частот, обнаружения и приёма слабых сигналов.

Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Харкевич А. А., Избр. труды, т. 2, М., 1973; Основы теории колебаний, под ред. В. В. Мигулина, 2 изд., М., 1988. Г. В. Белокопытов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.