- РАВНОВЕСИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- РАВНОВЕСИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ
-
состояние механич. системы, находящейся под действием сил, при к-ром все её точки покоятся по отношению к рассматриваемой системе отсчёта. Если система отсчёта явл. инерциальной (см. ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА), равновесие наз. абсолютным, а если неинерциальной, то относительным. Изучение условий Р. м. с.— одна из осн. задач статики. Условия Р. м. с. имеют вид равенств, связывающих действующие силы и параметры, определяющие положения системы; число этих условий равно числу степеней свободы системы. Условия относит. Р. м. с. составляются так же, как и условия абс. равновесия, но к действующим на точки силам прибавляют соответствующие переносные силы инерции. Условия равновесия свободного тв. тела состоят в равенстве нулю сумм проекций сил на три координатные оси Oxyz и сумм моментов всех приложенных к телу сил относительно этих осей, т. е.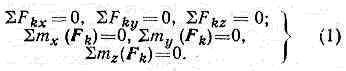 При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, напр. двигаться поступательно, равномерно и прямолинейно. Если тв. тело не явл. свободным (см. СВЯЗИ МЕХАНИЧЕСКИЕ), то условия его равновесия дают те из равенств (1) (или их следствий), к-рые не содержат реакций наложенных связей; остальные равенства дают ур-ния для определения неизвестных реакций. Напр., для тела, имеющего неподвижную ось вращения Oz, условием равновесия будет Smz(Fk)=0; остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жёстко, то все равенства (1) дают ур-ния для определения реакций связей.Согласно отвердевания принципу, равенства (1), не содержащие реакций внеш. связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механич. системы и, в частности, деформируемого тела. Необходимые и достаточные условия равновесия любой механич. системы могут быть найдены с помощью возможных перемещений принципа. Для системы, имеющей s степеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил.Из состояний равновесия, определяемых условиями (1) или (2), практически реализуются лишь те, к-рые явл. устойчивыми (см. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ). Равновесия жидкостей и газов рассматриваются в гидростатике и фэростатике.
При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, напр. двигаться поступательно, равномерно и прямолинейно. Если тв. тело не явл. свободным (см. СВЯЗИ МЕХАНИЧЕСКИЕ), то условия его равновесия дают те из равенств (1) (или их следствий), к-рые не содержат реакций наложенных связей; остальные равенства дают ур-ния для определения неизвестных реакций. Напр., для тела, имеющего неподвижную ось вращения Oz, условием равновесия будет Smz(Fk)=0; остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жёстко, то все равенства (1) дают ур-ния для определения реакций связей.Согласно отвердевания принципу, равенства (1), не содержащие реакций внеш. связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механич. системы и, в частности, деформируемого тела. Необходимые и достаточные условия равновесия любой механич. системы могут быть найдены с помощью возможных перемещений принципа. Для системы, имеющей s степеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил.Из состояний равновесия, определяемых условиями (1) или (2), практически реализуются лишь те, к-рые явл. устойчивыми (см. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ). Равновесия жидкостей и газов рассматриваются в гидростатике и фэростатике.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- РАВНОВЕСИЕ МЕХАНИЧЕСКОЙ СИСТЕМЫ
-
- состояние, при к-ром все точки механич. системы находятся в покое по отношению к рассматриваемой системе отсчёта. Если система отсчёта является инерциальной,
равновесие наз. абсолютным, в противном случае - относительным. Изучение условий Р. м. с.- одна из осн. задач статики. Условия Р. м. с. имеют вид равенств, связывающих действующие силы и параметры, определяющие положение системы; число этих условий равно числу степеней свободы системы. Условия относит. Р. м. с. составляются так же, как и условия абс. равновесия, если к действующим на точки системы силам прибавить соответствующие переносные силы инерции. Необходимые и достаточные условия равновесия свободного твёрдого тела состоят в равенстве нулю сумм проекций на три координатные оси Oxyz и сумм моментов относительно этих осей всех приложенных к телу сил, т. е.
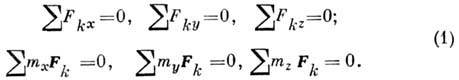
При выполнении условий (1) тело будет по отношению к данной системе отсчёта находиться в покое, если скорости всех его точек относительно этой системы в момент начала действия сил были равны нулю. В противном случае тело при выполнении условий (1) будет совершать т. н. движение по инерции, напр. двигаться поступательно, равномерно н прямолинейно, равномерно вращаться вокруг одной из своих гл. центр, осей инерции или совершать вокруг центра масс более сложное движение, в частности регулярную прецессию.
Если твёрдое тело не является свободным (см. Связи механические), то условия его равновесия дают те из равенств (1) (или их следствия), к-рые не содержат реакций наложенных связей; остальные равенства дают ур-ния для определения неизвестных реакций. Напр., для тела, имеющего неподвижную ось вращения Oz, условием равновесия будет
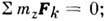 остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жёстко, то все равенства (1) дают ур-ния для определ. реакций связей. Такого рода задачи часто решаются в технике.
остальные равенства (1) служат для определения реакций подшипников, закрепляющих ось. Если тело закреплено наложенными связями жёстко, то все равенства (1) дают ур-ния для определ. реакций связей. Такого рода задачи часто решаются в технике.На основании отвердевания принципа равенства (1), не содержащие реакций внеш. связей, дают одновременно необходимые (но недостаточные) условия равновесия любой механич. системы, в частности деформируемого тела. Необходимые и достаточные условия равновесия любой механич. системы могут быть найдены с помощью возможных перемещений принципа. Для системы, имеющей s степеней свободы, эти условия состоят в равенстве нулю соответствующих обобщённых сил:
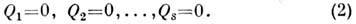
Из состояний равновесия, определяемых условиями (1) и (2), практически реализуются лишь те, к-рые являются устойчивыми (см. Устойчивость равновесия). Равновесия жидкостей и газов рассматриваются в гидростатике и аэростатике.
С. М. Тарг.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
