ПРЫЖКОВАЯ ПРОВОДИМОСТЬ

ПРЫЖКОВАЯ ПРОВОДИМОСТЬ

       

механизм электропроводности тв. тел, связанный с «перескоками» эл-нов, локализованных в пр-ве, из одного состояния в другое. П. п. наблюдается в неупорядоченных системах, у к-рых электронные состояния, локализованные в разных местах, имеют разную энергию. При прыжке эл-на из одного состояния в другое дефицит энергии покрывается за счёт энергии тепловых колебаний атомов. С этим связана характерная температурная зависимость электрич. сопротивления r. При умеренно низких темп-рах, когда доминируют «прыжки» между соседними состояниями, lnr=T-1. С понижением темп-ры длина прыжка возрастает, а дефицит энергии уменьшается. Это приводит к зависимости lnr=Tn, где n<1.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ПРЫЖКОВАЯ ПРОВОДИМОСТЬ

- низкотемпературный механизм проводимости в полупроводниках, при к-ром перенос заряда осуществляется путём квантовых туннельных переходов ("прыжков") носителей заряда между разл. локализованными состояниями. Прыжки сопровождаются поглощением или излучением фононов. Наиб. изучена П. п. в слаболегированном кристаллич. полупроводнике, где происходит туннелирование между примесными электронными состояниями, а также в аморфных и стеклообразных полупроводниках, в к-рых носители заряда туннелируют между локализов. состояниями хвоста плотности состояний в квазизапре-щённой зоне.

Слаболегированным наз. кристаллич. полупроводник (для определённости м-типа), в к-ром концентрация доноров N _д. мала по сравнению с концентрацией, при к-рой происходит переход металл - диэлектрик. В таких случаях перекрытие электронных оболочек соседних доноров мало. Поэтому каждый донор можно рассматривать как водородоподобный атом, внеш. электрон к-рого находится на расстоянии боровского радиуса a = 0,5·10^-8 см и имеет энергию связи с ядром 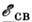~ 13,6 эВ. В таких полупроводниках переход к П. п. происходит при низких темп-pax ( Т~ 10 К), когда вероятность термоактивации электрона донора в зону проводимости (для определённости рассматриваем полупроводник n-типа) становится много меньше вероятности его туннелирования на соседний незанятый донор. 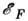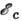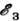На графике зависимости логарифма проводимости d от 1/ Т этому переходу соответствует излом (энергия активации проводимости меняется от - до , равной по порядку величины ширине примесной зоны 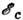- дно зоны проводимости).

Т. к. электрон может прыгать только с занятого донора на свободный, необходимым условием П. п. является наличие свободных мест в примесной зоне, к-рое при низких темп-pax может быть обеспечено лишь компенсацией, т. е. введением акцепторной примеси, забирающей часть электронов с доноров.

Модель сетки сопротивлений. При термодинамич. равновесии частоты Г _ij туннельных переходов электрона с донора i на донор j и обратно (Г _ji) равны между собой и определяются соотношением

i

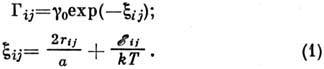
Здесь 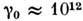Гц (частота порядка фононной), 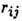- расстояние между донорами, а- радиус локализации волновой ф-ции электрона,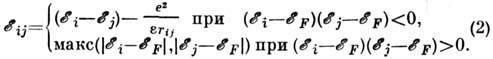

Здесь 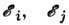- энергии электрона на донорах, e - диэлектрич. проницаемость. Первое слагаемое в (1) связано с зависимостью от 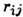матричного элемента электронно-фононного взаимодействия, второе - с малой вероятностью найти фонон с энергией больше kT, необходимый для перехода.

Внеш. электрич. поле Е нарушает баланс между Г _ij и Г _ji по двум причинам: 1) за счёт действия самого поля и за счёт изменения зарядового состояния соседних примесей меняются энергии доноров, а с ними и энергия фонона, необходимого для прыжка; 2) поле, перераспределяя электроны, меняет средние по времени числа заполнения доноров, что можно описать введением для каждого донора локального квазиуровня Ферми 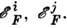В результате между донорами возникает электрич. ток, пропорциональный электрич. полю Е (линейное приближение):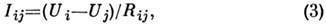

где 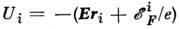- электрохим. потенциал.

Можно показать, что

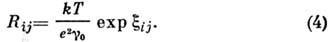
Т. о., задача о вычислении прыжковой электропроводности полупроводника сводится к задаче о проводимости эквивалентной сетки сопротивлений (сетки Миллера и Абрахамса), узлы к-рой соответствуют локализованным состояниям (донорам), а сопротивления, включённые между узлами, задаются (4).

Важнейшим свойством сетки Миллера и Абрахамса является экспоненциально широкий разброс входящих в неё сопротивлений: для слаболегированного полупроводника значения только первого слагаемого в (1) для доноров, отстоящих на среднем и двух средних расстояниях, отличаются примерно в 10, а соответствующие сопротивления R_ij в е¹⁰ (в 2,2·10⁴) раз. Поэтому для вычисления проводимости всей сетки необходимо использовать методы протекания теории, к-рые дают выражение для проводимости:

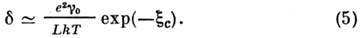
Здесь 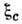- т. н. порог протекания по случайным узлам с критерием связности 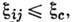при к-ром все пары доноров с 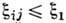образуют бесконечный кластер, пронизывающий весь образец. Длина кластера

где 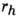- ср. длина прыжка, а 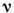- критич. индекс, зависящий от размерности решётки: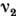= 1,33, 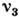= 0,88. Наиб. просто задача о вычислении 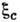решается для относительно высоких темп-р, когда для типичной пары ближайших доноров с 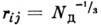первое слагаемое в (1) много больше второго. В этом случае

где 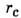= 0,865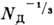- т. н. перколяционный радиус, а 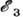=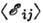. Ср. энергия 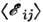определяется легированием и степенью компенсации образца К = N _А/N _Д(N _А - концентрация акцепторов):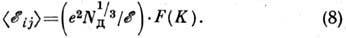

Здесь F(K) - безразмерная ф-ция (табулирована).

При К: 0 величина F(K)= 0,99; при росте степени компенсации F(K )сначала убывает, проходит через минимум при К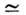0,5 и возрастает как 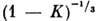при К: 1. При К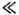1 ф-ла (7) справедлива при Т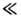T _кр 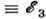/kln(l/K), а при Т > Т _кр проводимость зависит от Т лишь степенным образом.

Прыжковая проводимость с переменной длиной прыжка. При низких темп-pax, когда /kT > 2r _с/а, значит. вклад в П. п. дают не все локализов. состояния примесной зоны, а только их небольшая часть, попадающая в "оптимальную" энергетич. полоску 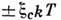вокруг уровня Ферми. При уменьшении Т ширина оптим. полоски уменьшается (несмотря на рост x _с), а расстояния между попавшими в неё локализов. состояниями растут; П. п. в этом режиме наз. П. п. с переменной длиной прыжка (VRH- variable range hopping). Если плотность состояний 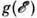постоянна внутри полоски, то для x _с справедлив закон Мотта: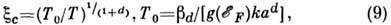

где d- размерность пространства, коэф. 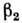= 13,8,

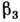= 21,2.

В слаболегированных полупроводниках, где основной причиной разброса энергетич. уровней является кулоновский потенциал заряженных примесей, плотность состояний на уровне Ферми квадратично обращается в 0 (кулоновская щель). В этом случае

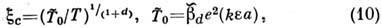
где 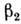= 6,2, 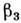= 2,8.

Прыжковая проводимость в аморфных полупроводниках практически всегда носит характер VRH и наблюдается при значительно более высоких темп-рах, чем в слаболегированных кристаллич. полупроводниках, из-за большей плотности состояний. Вид зависимости s(Т )определяется структурой 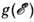и сильно зависит от материала и способа приготовления образца. У многих аморфных полупроводников наблюдается зависимость (10).

Неомические эффекты в П. п. наступают в электрич. полях, когда напряжение eEL, падающее на корреляционной длине бесконечного кластера, становится больше или порядка kT, н для критич. сопротивлений сетки Миллера и Абрахамса оказывается неверным выражение (3), полученное разложением по малому параметру eU/kT. При 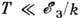и в области VRH электропроводность s(E)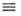j(Е)/Е экспоненциально растёт с полем. Для E> Е _с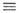k T/eL в пределе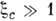

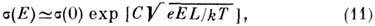
где С- численный коэф. Выражение (11) справедливо для x _с > 30, а при соответствующих эксперименту значениях 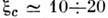зависимость ln[s(E)/s(0)] от E близка к линейной.

Прыжковая проводимость в переменном электрическом поле связана со смешением носителей лишь на конечные расстояния. Поэтому при частоте поля 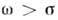проводимость определяется не бесконечным кластером, а переходами электронов между парами конечных кластеров, состоящих из доноров, связанных сопротивлениями с 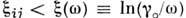. При больших частотах, когда разница x _с - x(w) становится не мала но сравнению с x_c, проводимость определяется поглощением энергии в изолиров. парах локализованных состояний. При относительно малых частотах и высоких темп-pax, когда 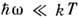, основным механизмом поглощения являются релаксац. потери, а при 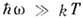- резонансное (бесфононное) поглощение фотонов.

Лит.: Шкловский Б. И., Неомическая прыжковая проводимость, "ФТП", 1976, т. 10, в. 8, с. 1440; Шкловский Б. И., Эфрос А. Л., Электронные свойства легированных полупроводников, М., 1979; Нгуен Ван Лиен, Шкловский Б. И., Эфрос А. Л., Энергия активации прыжковой проводимости слабо легированных полупроводников, "ФТП", 1979, т. 13, с. 2192; Звягин И. П., Кинетические явления в неупорядоченных полупроводниках, М., 1984.

Е. И. Левин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.