- ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
-
энергетич. характеристики эл.-магн. поля, к-рые вводят для описания поля наряду с силовыми хар-ками — напряжённостью электрич. поля Е и магн. индукцией В. В электростатике векторное электрич. поле можно характеризовать одной скалярной ф-цией — потенциалом электростатическим. В общем случае для описания произвольного эл.-магн. поля вместо Е и В можно ввести две др. величины: векторный потенциал А (х, у, z, t) и скалярный потенциал j(x, у, z, t), где х, у, z — координаты, t — время, при этом В и E однозначно выражаются через А и j: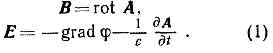 Ур-ния для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, что упрощает задачу нахождения переменных эл.-магн. полей. Существ. упрощение ур-ний для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы
Ур-ния для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, что упрощает задачу нахождения переменных эл.-магн. полей. Существ. упрощение ур-ний для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы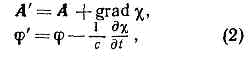 где c — произвольная ф-ция координат и времени, то векторы В и Е, определяемые ур-ниями (1), не изменятся. Инвариантность эл.-магн. поля по отношению к преобразованиям потенциалов (2) носит назв. к а л и б р о в о ч н о й, или г р а д и е н т н о й, и н в а р и а н т н о с т и. Калибровочная инвариантность позволяет наложить на П. э. п. дополнит. условие. Обычно таким дополнит. условием явл. условие Лоренца:
где c — произвольная ф-ция координат и времени, то векторы В и Е, определяемые ур-ниями (1), не изменятся. Инвариантность эл.-магн. поля по отношению к преобразованиям потенциалов (2) носит назв. к а л и б р о в о ч н о й, или г р а д и е н т н о й, и н в а р и а н т н о с т и. Калибровочная инвариантность позволяет наложить на П. э. п. дополнит. условие. Обычно таким дополнит. условием явл. условие Лоренца: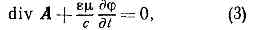 где e и m — диэлектрич. и магн. проницаемости среды. При использовании условия (3) ур-ния для П. э. п. в однородной среде (e=const, m=const), получаемые из ур-ний Максвелла, приобретают одинаковую форму:
где e и m — диэлектрич. и магн. проницаемости среды. При использовании условия (3) ур-ния для П. э. п. в однородной среде (e=const, m=const), получаемые из ур-ний Максвелла, приобретают одинаковую форму: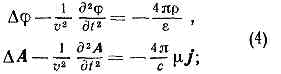 здесь D=д2/дx2+д2/дy2+д2/дz2— т. н. оператор Лапласа, r и j — плотности заряда и тока, a v=c/?em — скорость распространения эл.-магн. поля в среде. Если r=0 и j=0, то П. э. п. удовлетворяют волновому уравнению.Ур-ния (4) позволяют определить потенциалы A и j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) — и хар-ки эл.-магн. поля В и Е. Частные решения ур-ний (4), удовлетворяющие причинности принципу, наз. з а п а з д ы в а ю щ и м и п о т е н ц и а л а м и. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностями заряда и тока в точке с координатами х', у', z' в предшествующий момент времени t=t-R/v, где R=?((х-х')2+(у-у')2+(z-z')2)— расстояние от источника поля до точки наблюдения.Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы определяются интегрированием элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz', с учётом времени запаздывания:
здесь D=д2/дx2+д2/дy2+д2/дz2— т. н. оператор Лапласа, r и j — плотности заряда и тока, a v=c/?em — скорость распространения эл.-магн. поля в среде. Если r=0 и j=0, то П. э. п. удовлетворяют волновому уравнению.Ур-ния (4) позволяют определить потенциалы A и j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) — и хар-ки эл.-магн. поля В и Е. Частные решения ур-ний (4), удовлетворяющие причинности принципу, наз. з а п а з д ы в а ю щ и м и п о т е н ц и а л а м и. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностями заряда и тока в точке с координатами х', у', z' в предшествующий момент времени t=t-R/v, где R=?((х-х')2+(у-у')2+(z-z')2)— расстояние от источника поля до точки наблюдения.Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы определяются интегрированием элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz', с учётом времени запаздывания: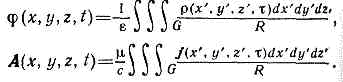 Через П. э. п, выражается Гамильтона функция (Н) заряженной ч-цы, движущейся в эл.-магн. поле:
Через П. э. п, выражается Гамильтона функция (Н) заряженной ч-цы, движущейся в эл.-магн. поле: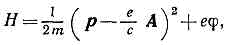 где р — импульс ч-цы, е и m — её заряд и масса. Соответственно через П. э. п. выражается оператор Гамильтона (гамильтониан) в квант. теории.
где р — импульс ч-цы, е и m — её заряд и масса. Соответственно через П. э. п. выражается оператор Гамильтона (гамильтониан) в квант. теории.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
-
- вспомогательные функции, через к-рые выражаются векторы, характеризующие эл.-магн. поле. Наиб. часто используются векторный потенциал
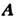 и скалярный потенциалf; через них может быть представлено решение двух однородных ур-ний Максвелла
и скалярный потенциалf; через них может быть представлено решение двух однородных ур-ний Максвелла 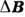 =0,
=0, 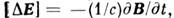 не содержащих источников поля в явном виде:
не содержащих источников поля в явном виде: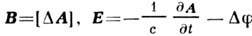
(использована гауссова система единиц). В среде, характеризующейся однородными электропроводностью
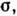 диэлектрической проницаемостью
диэлектрической проницаемостью 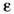 и магнитной проницаемостью
и магнитной проницаемостью  ур-ния для П. э. п. имеют вид
ур-ния для П. э. п. имеют вид 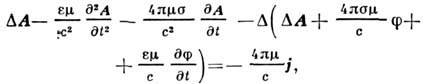
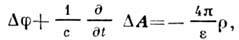
где j и r - объёмные плотности электрич. токов и зарядов. Неоднозначность введения потенциалов для одних и тех же эл.-магн. полей позволяет накладывать на П. э. п. дополнит. условия, наз. условиями калибровки (см. Градиентная инвариантность); это даёт возможность видоизменять (иногда упрощать) ур-ния для П. э. и.
Часто в задачах об излучении и распространении эл.-магн. волн в непоглощающих средах
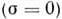 используется потенциал Герца (см. Герца вектор )Г, через к-рый выражаются векторный и скалярный потенциалы:
используется потенциал Герца (см. Герца вектор )Г, через к-рый выражаются векторный и скалярный потенциалы: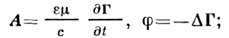
введённые т. о., они автоматически удовлетворяют условию калибровки Лоренца. Потенциал Герца удовлетворяет волновому ур-нию с электрич. поляризацией P. (плотностью электрич. дипольного момента) в качестве источника в правой части:
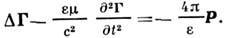
Пользуясь принципом двойственности, для полей, создаваемых источниками магн. типа
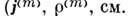 Максвелла уравнения), можно ввести сопряжённые обычным П. э. п. магнитные П. э. п.:
Максвелла уравнения), можно ввести сопряжённые обычным П. э. п. магнитные П. э. п.: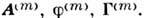
В задачах статики П. э. п.
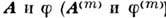 ) обычно используются независимо друг от друга.
) обычно используются независимо друг от друга.Лит. см. при ст. Максвелла уравнения.
М. А. Миллер, Е. В. Суворов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
