ОСЦИЛЛЯТОР

ОСЦИЛЛЯТОР

       

(от лат. oscillo -качаюсь), физическая система, совершающая колебания. Термином «О.» пользуются для любой системы, если описывающие её величины периодически меняются со временем.

К л а с с и ч е с к и й О.— механич. система, совершающая колебания около положения устойчивого равновесия (напр., маятник, груз на пружине). В положении равновесия потенц. энергия U системы имеет минимум. Если отклонения х от этого положения малы, то в разложении U(х) по степеням х можно принять U(x) = kx2/2 (k — постоянный коэфф.); при этом квазиупругая сила F=-dU/dx=-kx.

Такие О. наз. г а р м о н и ч е с к и м и, их движение описывается линейным ур-нием mx=-kx, решение к-рого имеет вид: х=Аsin(wt+j), где m — масса О., w=?k/m — частота, А — амплитуда колебаний, j — нач. фаза, t — время. Полная энергия гармонич. О, ?=mw2А2/2 — это сумма периодически меняющихся в противофазе кинетич. (Т) и потенц. энергий, ?=T+U не зависит от времени. Когда отклонение х нельзя считать малым, в разложении U(x) необходим учёт членов более высокого порядка — ур-ние движения становится нелинейным, а О. наз. а н г а р м о н и ч е с к и м.

Понятие О. применяется также к немеханич. колебат. системам. В частности, колебательный контур явл. алектрич. О. Колебания напряжённостей электрич. и магн. полей в плоской эл.-магн. волне также можно описывать с помощью понятия О.

Квантовый О. В квант. механике задача о линейном (с одной степенью свободы) гармонич. О. решается с помощью Шрёдингера уравнения (с U=kx2/2). Решение существует лишь для дискр. набора значений энергии ?n=ћ?(k/m(n+1/2)), n=0, 1, 2, ... Важной особенностью энергетич. спектра О. явл. то, что уровни энергии ?n расположены на равных расстояниях. Т. к. отбора правила разрешают в данном случае переходы только между соседними уровнями, то, хотя квант. О. имеет набор собств. частот wn=?n/ћ, излучение его происходит на одной частоте w, совпадающей с классической: w=?(k/m). В отличие от классич. О. наименьшее возможное значение энергии (при n=0) квант. О. равно не нулю, а ћw/2 (нулевая энергия).

Понятие О. играет важную роль в теории тв. тела, эл.-магн. излучения, колебат. спектров молекул.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ОСЦИЛЛЯТОР

(от лат. oscillo - качаюсь)- система (или материальная точка), совершающая колебательное периодич. <движение около положения устойчивого равновесия. Термин "О." применим клюбой системе, если описывающие её величины периодически изменяются современем. Простейшие примеры осциллятора в классической механике - грузикна пружинке, маятник.
Важнейший тип О. - линейный гармоническийосциллятор, колебания к-рого являются осн. моделью движения частиц в атомах, <атомных ядрах, молекулах, твёрдых телах. Потенц. энергия линейного гармония. <О. U = kx²/2, где x(t) - отклонение от положенияравновесия, k - пост. коэф. (в случае груза на пружинке k - жёсткостьпружины). Она представляет собой первый член разложения в ряд по х потенц. <энергии U(x )при малых х.
Ур-ние движения линейного гармонич. О. <имеет вид

где 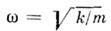- частота О., т - масса (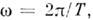где Т - период колебаний; точки означают дифференцирование по времени).Общее решение ур-ния (1):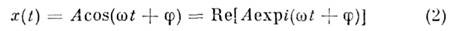

( А - амплитуда колебаний О.,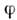- нач. фаза). Движение О., описываемое зависимостью (2), происходит подвлиянием возвращающей силы F, направленной к положению равновесияи пропорц. величине отклонения от положения равновесия: F = - дU/дx= - kx. При движении О. в пренебрежении силами трения его полная энергия

сохраняется. Кинетич. энергия 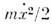и потенц. энергия kx²/2 в процессе движения изменяютсяот нуля до 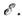Энергия колебаний О. может быть выражена через амплитуду и частоту:

Импульс О.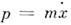меняется по тому же закону (2), что и х, но со сдвигом по фазе на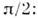

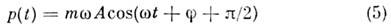
(соответственно кинетич. и потенц. энергииО. изменяются в противофазе). Если изобразить движение О. на фазовой плоскости, <по оси абсцисс к-рой отложена координата, а по оси ординат - импульс, тоего периодпч. движение происходит по эллипсу

с полуосями соответственно А и
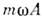
Понятие "О." распространяется и на немеханич. <системы: колебания тока и напряжения в колебат. контуре, колебания векторовнапряжённостей электрич. и магн. нолей в эл.-магн. волне и т. д.
Квантовый О. описывается гамильтонианом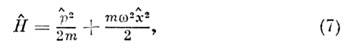

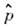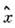где и - операторыимпульса и координаты; в конфигурац. представлении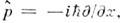 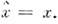Уровни энергии квантового О. эквидистантны: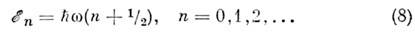

Они определяются из Шрёдитера уравнения

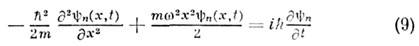
и изображаются обычно на кривой потенц. <энергии О. ( рис.), а волновые ф-ции 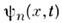стационарных состояний О. выражаются через полиномы Эрмита Н _п (см. Ортогональныеполиномы):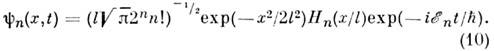

Здесь l - амплитуда нулевых колебаний, 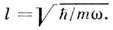В осн. состоянии О. с волновой ф-цией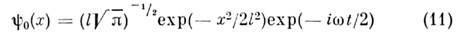

его энергия (энергия нулевых колебаний)имеет наинизшее возможное значение 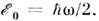В стационарных состояниях О. ср. значения координаты и импульса равны нулю. <Согласно Эренфеста теореме, ср. значения координаты и импульса гармонич. <О. изменяются в соответствии с классич. траекториями. Наглядно это движениепроявляется в нормированных когерентных состояниях О.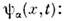

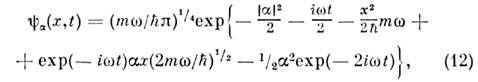
удовлетворяющих нестационарному ур-ниюШрёдингера и являющихся собств. состояниями для неэрмитового интеграладвижения (оператора уничтожения)

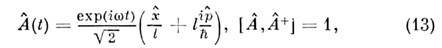
С комплексным собств. значением 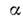:В когерентном состоянии 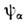ср. значения координаты 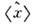и импульса 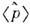,как и в классич. механике, описывают в фазовом пространстве эллипс. Операторуничтожения 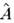и оператор рождения 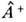действуют на n -е состояние след. образом: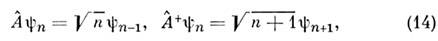

т. е. соответственно уничтожают и рождаютквант энергии О. Через операторы рождения и уничтожения гамильтониан гармонич. <О. выражается так:

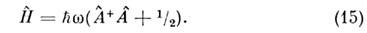
Важность модели О. заключается в том, чтовсе совр. модели квантовой теории поля базируются на многомерном(бесконечномерном) обобщении этого выражения:

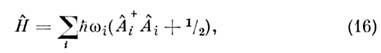
где индекс i трактуется как характеристикамоды поля (эл.-магн., акустического и т. д., т. е. фотона, фонона и т. <п.), а операторы 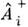,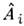- как операторы рождения и уничтожения кванта бозонного поля. К этой жемодели сводятся движение заряда в магн. поле, изменение тока и напряженияв колебат. контуре, колебания ядер в многоатомных молекулах и атомов имолекул в твёрдых телах, колебат. движение нуклонов в ядрах и т. д.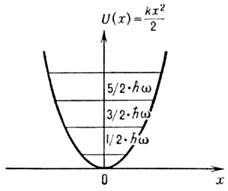

При учёте затухания ур-ние движения (1)О. принимает вид

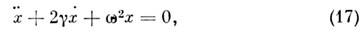
где 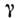- коэф. затухания, а движение О. представляет собой затухающие колебанияоколо положения равновесия: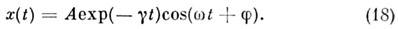

В квантовой картине затухание колебанийО. описывается неск. моделями, одна из к-рых базируется на гамильтониане

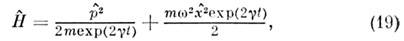
причём во всех моделях ср. значения координатыО. описываются ф-лой (18), а для др. величин в рамках разных моделей имеютсяразличия. Если на О. действует внеш. периодическая (с частотой 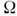)сила 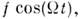то возникаютвынужденные колебания О. на частоте вынуждающей силы, описываемые ф-лой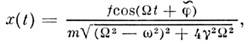

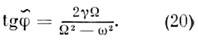
Резкое возрастание амплитуды вынужденныхколебаний при сближении собств. частоты О. и частоты вынуждающей силы наз. <резонансом гармония. О. Коэф. затухания определяет сдвиг фазы 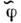колебаний О. по отношению к вынуждающей силе, равный 0 при отсутствии затуханияи 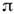/2 врезонансе. Для квантового аналога О. с затуханием также существует резонанс. <Под влиянием внеш. силы f(t )квантовый О. может переходить с одногоуровня энергии ( п )на другие ( т). Вероятность этого перехода W_nm(t )дляО. без затухания даётся ф-лой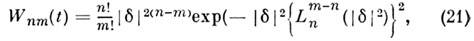

где

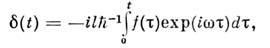
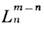- полиномы Лагерра (см. Ортогональные полиномы). Правила отборадля О. определяются ненулевыми матричными элементами оператора координаты(дипольное приближение). Согласно ф-лам (13), (14), эти элементы отличныот нуля только для переходов между соседними уровнями, поэтому излучениеО. происходит на одной частоте (совпадающей с классической,=).
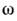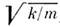Если потенц. энергия О. содержит членытипа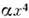 , 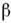х⁶ ит. д., то О. наз. ангармоническим (нелинейным) и характер его движениярадикально отличается от даваемого ф-лой (2). Если частота гармонич. О. <меняется со временем, то О. наз. параметрическим, для к-рого также характерколебаний отличен от (2), причём существуют новые явления, напр. параметрич. <резонанс О.

Лит.: Ландау Л. Д., Лифшиц Е. М.,Квантовая механика, 4 изд., М., 1989; их же, Механика, 4 изд., М., 1988,с. 207; Малкин И. А., Манько В. И., Динамические симметрии и когерентныесостояния квантовых систем, М., 1979.

В. И. Манъко.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.