ОРБИТАЛЬНЫЙ МОМЕНТ

ОРБИТАЛЬНЫЙ МОМЕНТ

       

момент импульса микрочастицы, обусловленный её движением в силовом поле, обладающем сферической симметрией. Название «О. м.» связано с наглядным представлением о движении ат. эл-на в сферически симметричном поле ядра по определённой замкнутой орбите.

Согласно квант. механике, О. м. ML квантован, т. е. его величина, а также проекция на произвольно выбранную в пр-ве ось (ось z) могут принимать лишь определённые дискр. значения: M2l=ћ2l(l+1), Mlz = mtћ, где l=0, 1, 2,...— орбитальное (азимутальное), а m=-1, l-1, . . . , -l — магнитное квантовые числа. Классификация состояний микрочастиц по значениям l играет большую роль в теории атома и ат. ядра, в теории столкновений.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ОРБИТАЛЬНЫЙ МОМЕНТ

(моментколичества движения) - динамич. характеристика движения частицы или механич. <системы, связанная с вращением. В классич. механике О. м. системы частиц(материальных точек) относительно центра О равен

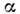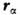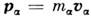где индекс нумеруетчастицы,и - радиус-вектор (проведённый из начала координат О )и импульс 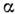-йчастицы ( 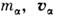-масса и скорость частицы). Из изотропии пространства следует, что при произвольномдвижении замкнутой системы вектор L сохраняется по величине и направлению(закон сохранения момента). Значение О. м. зависит, вообще говоря, от выбораначала координат. А именно, при сдвиге на вектор 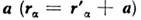имеем L = L' + [ аP], (2) где 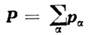- полный импульс системы. На законе сохранения О. м. эта неоднозначностьне сказывается, т. к. у замкнутой системы полный импульс Р такжесохраняется. В этом случае, когда Р = 0 (т. е. система как целоепокоится), её О. м. не зависит от выбора начала координат.
Компоненты О. м. имеют след. скобки Пуассона: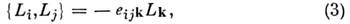

где e_ijk - полностью антисимметричный тензор ( е₁₂₃ =1;значения i =1,2,3 соответствуют осям х, у, z). Для системычастиц, находящейся под действием внеш. сил, изменение О. м. во временисвязано с полным моментом внеш. сил N:

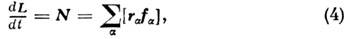
где 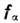- сила, приложенная к 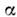-йчастице. В этой сумме должны учитываться только внеш. силы, т. к. суммамоментов всех сил, действующих внутри замкнутой системы, всегда равна нулю.
При переходе к квантовой механике переменные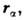 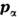заменяются операторами 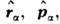причём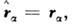 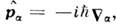где 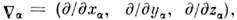а О. м. - оператором 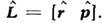Соотношение (3) заменяется коммутатором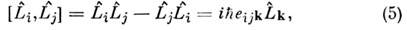

из к-рого следует, что разл. компонентыоператора О. м.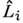не коммутируют между собой и поэтому, в соответствии с общими принципамиквантовой механики, компоненты момента L_i не являютсяодновременно измеримыми величинами (за исключением случая L = 0,когда все компоненты О. м. также имеют нулевые значения). Поскольку 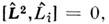то одновременно измеримы квадрат О. м. и одна из его компонент, в качествек-рой обычно выбирают L_z. Возможные наблюдаемые значенияэтих величин совпадают с собств. значениями 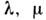соответствующих операторов и определяются из ур-ний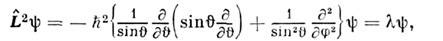

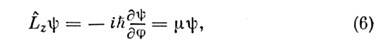
где 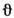и 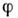- углыв сферич. системе координат, причём 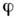- угол поворота вокруг оси z (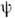- собств. ф-ции операторов 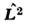и 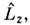общиедля обоих операторов). Однозначные и всюду ограниченные (на единичной сфере)решения этих ур-ний существуют только при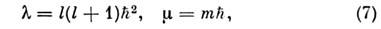

где l (т. н. орбитальное, или азимутальное, <квантовое число) принимает значения l = 0, 1, 2, 3,..., а т (магн. квантовое число) определяет величину проекции О. м. на ось . и принимает 2l+ 1 значений: m = l, l -1, ...,- l, что даёт кратность вырождения уровней энергии с данным l, равную 2l+ 1. Т. о., в квантовой механике возникает квантованиеО. м.
Решения ур-ния (6) совпадают со сферическимифункциями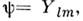

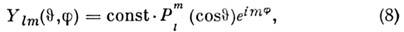
где 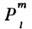- присоединённые полиномы Лежандра. В простейших случаях l = 0 (S- состояние)и l= 1 (P -состояние) Y_lm выражаются след. <образом: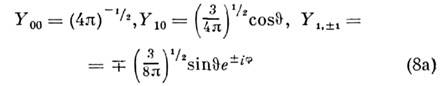

[в литературе встречаются и др. определения Y_lт, отличающиеся от (8а) фазовыми множителями]. Сферич. <ф-ции образуют ортонормированную систему:

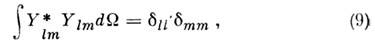
где 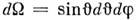- элемент телесного угла, а интегрирование ведётся по единичной сфере (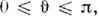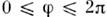), 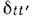-символ Кронекера. Величина 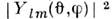определяет угловую зависимость плотности вероятности пространственногораспределения для частицы, находящейся в состоянии с квантовыми числами l, т.
О. м. и квантовое число l играютважную роль в классификации состояний квантовых систем. Электрон в атомедвижется в результирующем, самосогласованном поле, к-рое возникаетпри сложении кулоновского поля ядра и полей остальных электронов. Приближённоможно считать, что это ноле является сферически-симметричным, и пренебречь спин-орбитальным взаимодействием (что справедливо для не слишкомтяжёлых атомов). В этом случае квантовые состояния электрона в атоме характеризуютсяопредел. значениями l. В сферич. ядре состояния нуклона, движущегосяв усреднённом поле остальных нуклонов, также характеризуются значениями l (ядерные оболочки). Даже в тех случаях, когда потенциал взаимодействияне является сферически-симметричным и, следовательно, О. м. не сохраняется(т. е. не имеет вполне определ. значения), состояния с определёнными l,. часто используются в качестве базиса для разложения волновой ф-ции. <Во мн. случаях это является эфф. методом численного решения Шрёдингерауравнения для потенциалов, не обладающих сферич. симметрией.
Классификация квантовых состояний частицыпо значениям l встречается в теории атома, теории ядра и ядерныхреакций, теории столкновений, физике элементарных частиц и др.
О. м. микрочастицы (электрон, атом, ядрои т. д.) связан с её движением в пространстве. Помимо О. м., микрочастица, <как правило, обладает внутренним, или спиновым, моментом s, имеющим чистоквантовое происхождение (спин исчезает при переходе к пределу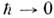 и не допускает классич. интерпретации). При наличии спина из изотропиипространства следует, что сохраняются не l и s по отдельности, <а лишь полный момент j = l + s (см. Квантовое сложениемоментов). При этом собств. значения оператора 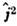равны 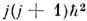Волноваяф-ция с определ. значениями j² и j_z может быть построена из координатной и спиновой волновых ф-ций с помощью Клебша- Гордана коэффициентов. Имеются отбора правила для переходовмежду состояниями с определёнными l и j, к-рые играют важнуюроль в теории эл.-магн. переходов в атомах и ядрах, при рассмотрении распадовэлементарных частиц и т. д.

Лит.: Ландау Л. Д., Лифшиц Е. М.,Квантовая механика. Нерелятивистская теория, 4 изд., М., 1989; их же, Механика,4 изд., М., 1988; Варшалович Д. А., Москалев А. Н., Херсонский В. К., Квантоваятеория углового момента, Л., 1975.

В. С. Попов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.