ОБРАТНАЯ РЕШЕТКА

ОБРАТНАЯ РЕШЕТКА

       

соответствующая данной (атомной) кристаллической решётке точечная трёхмерная решётка в абстрактном (обратном) пр-ве, в к-ром расстояния имеют размерность обратной длины. Кристаллич. решётке с векторами трансляции а1, a2, a3 соответствует О. р., векторы трансляции к-рой равны: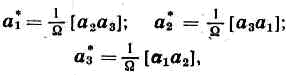

где W=a1(a2a3) — объём элем. ячейки исходной решётки. Вектор в О. р. Hhkl=ha*1+ka*2+la*3 перпендикулярен плоскости с индексами кристаллографическими hkl. Элем. ячейка О. р. имеет объём W-1, обратный объёму элем. ячейки кристалла. Понятие О. р. и обратного пространства широко применяется при описании явлений дифракции и распространения волн и ч-ц в кристаллах, в теории тв. тел при анализе энергетич. спектров эл-нов, фононов и др. квазичастиц (см. ДИФРАКЦИЯ МИКРОЧАСТИЦ, ЭЛЕКТРОНОГРАФИЯ, НЕЙТРОНОГРАФИЯ, РЕНТГЕНОВСКИЙ СТРУКТУРНЫЙ АНАЛИЗ).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ОБРАТНАЯ РЕШЁТКА

- периодпч. решёткав обратном пространстве, элементарные векторы трансляции к-рой b_i связаны с осн. векторами трансляции a_i исходной Браве решётки (прямой решётки) условиями

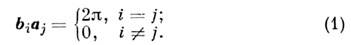
Узлы О. р. задаются соотношениями 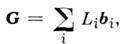где L_i- произвольные целые числа, i =1, 2, 3 для трёхмерной решётки,i= 1, 2 для двухмерной. Размерность О. р. совпадает с размерностьюпрямой решётки. Так, для трёхмерной прямой решётки О. р. является трёхмернойс элементарными векторами трансляции, равными в соответствии с (1):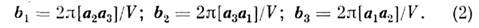

Здесь V =( а ₁[ а₂ а₃])- объём элементарной ячейки прямой решётки; объём элементарной ячейки О. <р. равен 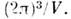Вектор О. p. G_hkl= hb₁ + kb₂+ lb₃ перпендикулярен плоскости с индексамикристаллографическими h, k, l.
Между прямыми и О. р. имеется взаимнооднозначное соответствие, причём прямая решётка является обратной к обратной. <Поэтому для каждого кристалла О. р. вводится однозначно, а симметрия О. <р. полностью определяется симметрией решётки Браве кристалла. Напр.. О. <р. для простой кубич. решётки - простая кубическая, для гранецентрир. кубической- объёмно-центрир. кубическая (и наоборот) и т. д.
Понятие О. р. является одним из основныхв физике твёрдого тела. О. р. определяет структуру пространства квазиимпульсов квазичастиц. Их волновые векторы определены с точностью до векторовтрансляции О. p. G; состояния квазичастиц, для которых квазиимпульсыотличаются на величину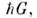 а остальные квантовые числа одинаковы, тождественны. Поэтому область всехфизически неэквивалентных значений волнового вектора квазичастицы образуетэлементарную ячейку О. р. Соответственно энергетич. спектр квазичастици др. ф-ции волнового вектора являются периодич. ф-циями векторов трансляцииО. р. При этом мн. характеристики квазичастиц кристалла могут задаватьсяразложением в ряд Фурье по векторам трансляции О. р. Это позволяет перейтик квазиимпульсному представлению для операторов и волновых ф-ций квазичастицпо аналогии с переходом к импульсному представлению для частиц в свободномпространстве (см. Импульсное представление в квантовой механике).
Экстремумы энергетич. спектра обычно соответствуютточкам высокой симметрии ячеек О. р. При столкновениях квазичастиц суммаих квазиимпульсов сохраняется с точностью до G (см. Перебросапроцессы). Вигнера - Зейтца ячейка О. р. является первой Бриллюэназоной для кристалла.
О. р. - важный матем. образ, находящиймногочисл. применения в кристаллографии и физике твёрдого тела. Напр.,понятие О. р. удобно использовать при описании дифракции частиц на кристаллич. <решётке (см. Дифракция нейтронов, Нейтронография структурная, Рентгеновскийструктурный анализ, Электронография). Соответственно нейтроно- и рентгенограммыкристалла могут дать "изображение" О. р.

Лит.: Ландау Л. Д., Лифшиц Е. М.,Статистическая физика, ч. 1, 3 изд., М., 1976; Современная кристаллография, <т. 1, М., 1979.

А. Э. Мейерович,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.