МУТНЫЕ СРЕДЫ

МУТНЫЕ СРЕДЫ

       

среды с оптич. неоднородностями, на к-рых происходит рассеяние света. Оптич. неоднородности могут быть связаны с включением одного в-ва в другое (облака, туманы, дымы, эмульсии) и с флуктуациями плотности и анизотропии вследствие теплового движения (см. РАССЕЯНИЕ СВЕТА). Это приводит к образованию микрообластей с показателем преломления, отличным от показателя преломления окружающей среды (напр., опалесценция критическая). В общем случае излучение, рассеянное М. с., состоит из лучей с разл. кратностью рассеяния. Однократное рассеяние света наблюдается при малой оптической толщине т. С увеличением т кратность рассеяния растёт, поскольку растёт вероятность облучения каждой из оптич. неоднородностей светом, рассеянным др. неоднородностями. Закономерности однократного и многократного светорассеяния существенно различны. Оптич. хар-ки М. с. с однократным рассеянием определяются размером оптич. неоднородностей (точнее, отношением размера к длине волны рассеиваемого излучения l), их относит. показателем преломления, формой и числом в ед. объёма. Многократное рассеяние света в М. с. обусловлено помимо их структуры и такими факторами, как протяжённость, форма и границы всей среды в целом. Закономерности многократного рассеяния света сложны и меняются в зависимости от оптич. толщины. Полная хар-ка многократно рассеянного света даётся решением ур-ния переноса излучения.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

МУТНЫЕ СРЕДЫ

- среды, в к-рых распространение света сопровождается значит. рассеянием, влияющим на условия распространения, вследствие чего нарушается прозрачность среды. Рассеяние света в среде происходит на её оптич. неоднородностях, что было установлено Л. И. Мандельштамом в 1907. Среда может быть мутной вследствие неоднородности структуры, наличия в ней посторонних макроскопич. частиц и включений (дымы, туманы, облака, коллоидные растворы). Флуктуации плотности, возникающие из-за теплового движения частиц, могут привести к резкому увеличению рассеяния, и среда станет сильно мутной ( опалесценция критическая). Среда может стать мутной при резонансном рассеянии.

В M. с. оптич. неоднородности распределены хаотично. Среды, в к-рых оптич. свойства изменяются плавно (локально однородные), света не рассеивают: внутри такой среды происходит постепенное искривление световых лучей (рефракция света).

Оптич. свойства M. с. определяются явлениями ослабления проходящего излучения вследствие рассеяния и поглощения и взаимного облучения разл. объёмов M. с. рассеянным излучением. Взаимное облучение имеет когерентную и некогерентную части. Когерентная часть взаимного облучения неоднородностей ведёт к изменению эфф. эл.-магн. поля, в к-ром они находятся, а следовательно, и рассеянного ими поля. Когерентная часть взаимного облучения и интерференция излучений, рассеянных различными объёмами, относятся к т. н. кооперативным эффектам, к-рые ведут к отличию оптич. свойств M. с. от оптич. свойств образующих её частиц. Некогерентная часть взаимного облучения неоднородностей или объёмов среды представляется в форме многократного рассеяния.

Теория рассеяния света в M. с. принципиально не отличается от дифракц. задач электродинамики: при известном внеш. излучении (освещении) и при известном пространственном распределении эл.-магн. свойств M. с. нужно определить поле в нек-рой точке вне или внутри среды.

Эту задачу можно представить состоящей из двух частей: 1) определить поле, рассеянное отд. элементом M. с., предполагая внеш. поле, в к-ром находится "мутный элемент", суперпозицией облучающего поля и поля, создаваемого всеми остальными элементами тела; 2) просуммировать действие всех элементов (частиц) тела (см. Рассеяние света).

В большинстве реальных M. с. эту общую задачу удаётся свести к более простым случаям, определяемым соотношением с длиной волны l след. четырёх линейных величин: d - расстояния между "элементами" (молекулами, микровключениями) внутри частицы, а - размера частицы, l - ср. расстояния между центрами частиц в M. с., R - размера M. с. Конкретная задача и метод её решения определяются величинами четырёх безразмерных параметров: х₁ = d/l, x₂ = a/l, x₃= = l/l, x₄ = R/l. Параметры x_i удовлетворяют очевидным неравенствам x₁.< х₂< x₃< x₄. Обычно также x₁ << 1 и x₄ >> 1.

Если параметр х₃>> 1, т. е. расстояние между частицами l>> l, то отд. частицы среды рассеивают свет некогерентно. В этом случае задача сводится к анализу однократного рассеяния на частице, к-рое зависит от величины х₂. (размера частицы) и относительного комплексного показателя преломления частицы n= n' - i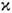. При очень малых размерах частицы ( х₂<< 1 и | п| 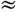1) наблюдается рэлеевское рассеяние. При этом показатель рассеяния приблизительно 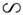l^-4, т. е. синие лучи, напр., рассеиваются в 16 раз сильнее, чем красные. Поэтому прямой свет от Солнца кажется красным, а небо - от рассеянного света Солнца - синим.

Более общий случай любых х₂. был рассмотрен А. Лявом (A. Love, 1899) и Г. Ми (G. Mie, 1908) (см. Mu тео рия). Расчёт светового поля для случая больших x₂ (до ~10³) очень сложен и осуществляется на ЭВМ. Однако картина поля, получающаяся из расчётов, хорошо совпадает с той, что следует из простых ф-л геом. оптики.

Если параметр x₃< 1, то волны, рассеянные разными частицами, уже нельзя считать некогерентными, большую роль начинает играть интерференция между рассеянными волнами ("кооперативные эффекты").

Для M. с., оптическая толщина к-рой т не мала (т =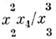> 1), наряду с однократным важное значение имеет также многократное рассеяние, воспринимаемое как самоосвещение среды. В результате мн. рассеяний при прохождении сквозь оптически толстую среду параллельный пучок света превращается в диффузный, источник света сквозь мутный слой не виден. Вследствие статистич. характера этого процесса, он описывается не напряжённостями полей, а матрицей плотности или Стокса параметрами, аддитивными для некогерентных пучков. Многократное рассеяние описывается также ур-нием переноса излучения.

Если параметр x₃<< 1, то M. с. можно рассматривать как квазисплошное тело. Этот метод был предложен Дж. Максвеллом-Гарнетом (J. Maxwell-Garnett, 1904) и широко используется в оптике коллоидов, гетерогенных твёрдых тел и др.

Четыре безразмерных параметра, отмеченных выше, достаточны для классификации M. с. в поле бесконечно плоской когерентной волны. Реальные пучки лишь частично когерентны, и их рассеяние зависит ещё от длины когерентности r, точнее от пятого параметра x₅ = = r/l. Поскольку этот параметр характеризует статистич. свойства поля, а оно определяется свойствами источника света и пути, к-рый прошла волна до того, как попала на M. с., то его значение никак не связано с предыдущими четырьмя параметрами. Длина когерентности r = l²/Dl, где Dl - спектральная ширина излучаемой линии. При учёте частичной когерентности света исследование "кооперативных эффектов" становится особенно сложной задачей.

Лит.: Шифрин К. С., Рассеяние света в мутной среде, M.- Л., 1951; Соболев В. В., Рассеяние света в атмосферах планет, M., 1972. К. С. Шифрин.

М-ЧИСЛО - то же, что Маха число.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.