- МАГНИТНЫЙ ПОТОК
- МАГНИТНЫЙ ПОТОК
-
(поток магнитной индукции), поток Ф вектора магн. индукции В через к.-л. поверхность. М. п. dФ через малую площадку dS, в пределах к-рой вектор В можно считать неизменным, выражается произведением величины площадки и проекции Bn вектора на нормаль к этой площадке, т. е. dФ=BndS. М. п. Ф через конечную поверхность S определяется интегралом: Ф=?SBndS.Для замкнутой поверхности этот интеграл равен нулю, что отражает соленоидальный хар-р магнитного поля, т. е. отсутствие в природе магнитных зарядов — источников магн. поля (магн. поля создаются электрич. токами). Единица М. п. в Международной системе единиц (СИ) — вебер, в СГС системе единиц — максвелл; 1 Вб=108 Мкс.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МАГНИТНЫЙ ПОТОК
-
- поток Ф вектора магнитной индукции В через к.-л. поверхность S:

Здесь dS - элемент площади, п - единичный вектор нормали к S. В СИ М. п. измеряется в веберах (Во), в гауссовой системе единиц (к-рая применяется ниже) - в максвеллах (Мкс); 1 Вб=108 Мкс. Поскольку вектор В является чисто вихревым
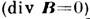 , М. п. через произвольную замкнутую поверхность S равен нулю. Это свойство, установленное Гауссом, может нарушаться только при наличии внутри S магнитных монополей, пока ещё гипотетических.
, М. п. через произвольную замкнутую поверхность S равен нулю. Это свойство, установленное Гауссом, может нарушаться только при наличии внутри S магнитных монополей, пока ещё гипотетических.
Изменение во времени М. п. ведёт, согласно Максвелла уравнениям (в интегральной форме), к возникновению вихревого электрич. поля Е, циркуляция к-рого по замкнутому контуру l, ограничивающему поверхность S, равна
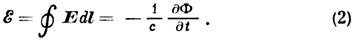
Здесь направление обхода по l связано с направлением нормали п к S правилом правого винта.
Для проводящих контуров, изготовленных из материалов с достаточно высокой проводимостью (напр., из металлич. провода), соотношение (2) в квазистатич. приближении соответствует закону электромагнитной индукции Фарадея:
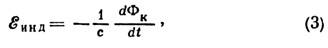
где -эдс эл.-магн. индукции,
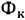 - М. п., "сцепленный"
- М. п., "сцепленный" 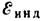 с проводящим контуром, т. е. М. п., усреднённый по всем поверхностям Si, опирающимся на линии тока в контуре. В отличие от (2), в (3) берётся полная производная от М. п. по времени в соответствии с тем, что эдс индукции возникает не только при изменении магн. поля во времени, но и при движении проводящего контура поперёк магн. поля, при вращениях и деформациях контура.
с проводящим контуром, т. е. М. п., усреднённый по всем поверхностям Si, опирающимся на линии тока в контуре. В отличие от (2), в (3) берётся полная производная от М. п. по времени в соответствии с тем, что эдс индукции возникает не только при изменении магн. поля во времени, но и при движении проводящего контура поперёк магн. поля, при вращениях и деформациях контура.
М. п., сцепленный со свсрхпроводящим контуром, постоянен во времени и может принимать лишь дискретные (квантованные) значения:
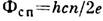 , где h - постоянная Планка, е - заряд электрона, и - целое число (см. Квантование магнитного потока). Величина кванта М. п. указывает на то, что носители электрич. тока в сверхпроводнике (куперовские пары) имеют заряд 2е.
, где h - постоянная Планка, е - заряд электрона, и - целое число (см. Квантование магнитного потока). Величина кванта М. п. указывает на то, что носители электрич. тока в сверхпроводнике (куперовские пары) имеют заряд 2е.
М. п. может направляться стержнями (обычно ферромагнитными) с магнитной проницаемостью
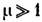 (см. Магнитная цепь), подобно тoму как электрич. ток направляется проводами с большой электропроводностью. На границе магнитопровода с окружающим пространством (вакуумом) непрерывна нормальная компонента вектора магн. индукции:
(см. Магнитная цепь), подобно тoму как электрич. ток направляется проводами с большой электропроводностью. На границе магнитопровода с окружающим пространством (вакуумом) непрерывна нормальная компонента вектора магн. индукции: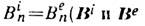 - внутр. и внеш. поле магн. индукции), а тангенциальная составляющая терпит скачок:
- внутр. и внеш. поле магн. индукции), а тангенциальная составляющая терпит скачок: 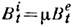 . Поэтому при
. Поэтому при 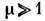 и при почти произвольной ориентации внеш. магн. поля (исключение составляет случай, когда поле нормально к границе) вектор магн. индукции
и при почти произвольной ориентации внеш. магн. поля (исключение составляет случай, когда поле нормально к границе) вектор магн. индукции 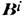 почти параллелен границе и его величина много больше
почти параллелен границе и его величина много больше 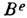 , а М. п. слабо меняется вдоль магнитопровода. Это свойство ферромагн. материалов широко используется в электротехнике для сосредоточения и переноса М. и. (напр., в трансформаторах, пост. магнитах, якорях электродвигателей).
, а М. п. слабо меняется вдоль магнитопровода. Это свойство ферромагн. материалов широко используется в электротехнике для сосредоточения и переноса М. и. (напр., в трансформаторах, пост. магнитах, якорях электродвигателей).
Лит.: Тамм И. Е., Основы теории электричества, 9 изд., М., 1976; Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982.
М. А. Миллер, Г. В. Пермитин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
