МАГНИТНЫЙ МОМЕНТ

МАГНИТНЫЙ МОМЕНТ

       

основная величина, характеризующая магн. свойства в-ва. Источником магнетизма (М. м.), согласно классич. теории эл.-магн. явлений, явл. макро- и микро(атомные)- электрич. токи. Элем. источником магнетизма считают замкнутый ток. Из опыта и классич. теории эл.-магн. поля следует, что магн. действия замкнутого тока (контура с током) определены, если известно произведение силы тока i на площадь контура s (M=is/с в СГС системе единиц). Вектор М и есть, по определению, М. м. Его можно записать по аналогии с электрическим дипольным моментом в форме: M=ml, где т — эквивалентный магнитный заряд контура, а l — расстояние между «магн. зарядами» противоположных знаков.

М. м. обладают элем. ч-цы, ат. ядра, электронные оболочки атомов и молекул. М. м. отдельных элем. ч-ц (эл-нов, протонов, нейтронов и др.), как показала квант. механика, обусловлен существованием у них собств. механич. момента — спина. М. м. ядер складываются из спиновых М. м. протонов и нейтронов, образующих эти ядра, а также из М. м., связанных с их орбит. движением внутри ядра. М. м. ат. ядер на три порядка меньше М. м. эл-нов в атомах, поэтому М. м. атомов и молекул определяется в осн. спиновыми и орбитальными М. м. эл-нов. Спиновый М. м. эл-на mсп может ориентироваться во внеш. магн. поле так, что возможны только две равные и противоположно направленные проекции mсп на направление вектора напряжённости Н внеш. поля: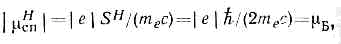

где ?е? — абс. значение элем. электрич. заряда, me — масса покоя эл-на, mБ — магнетон Бора, SH — проекция на H спинового механич. момента. Исследования ат. спектров показали, что mcn фактически равен не mБ, а mБ(1+0,0116). Это обусловлено действием на эл-н т. н. нулевых колебаний эл.-магн. поля (см. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА).

Орбитальный М. м. эл-на mорб связан с его орбит. механич. моментом

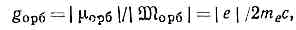где gорб — магнитомеханическое отношение для орбит. движения эл-на. Квант. механика допускает лишь дискр. ряд возможных проекций mорб на направление внеш. поля (см. КВАНТОВАНИЕ ПРОСТРАНСТВЕННОЕ): mop6=ml•mБ, где ml — магнитное квантовое число, принимающее 2l+1 значений (0, ±1, ±2, ..., ±l, где l — орбит. квант. число). В атомах суммарные орбитальный и спиновый М. м. эл-нов определяются отдельно квант. числами L и S. Сложение этих моментов проводится по правилам пространств. квантования. В силу неравенства магнитомеханич. отношения для спина эл-на и его орбит. движения результирующий М. м. электронной оболочки атома не будет параллелен или антипараллелен её результирующему механич. моменту.

Для хар-ки магн. состояния макроскопич. тел вычисляется ср. значение результирующего М. м. всех образующих тело микрочастиц. Отнесённый к ед. объёма тела М. м. наз. намагниченностыо. Для макроскопич. гол, особенно для тел с магнитной структурой атомной (ферро-, ферри- и антиферромагнетиков), вводят понятие средних атомных М. м. как ср. значениям, м., приходящегося на один атом (ион) — носитель М. м. Обычно средние атомные М. м. отличаются от М. м. изолированных атомов; их значения в mБ оказываются дробными (напр., у Fe, Co и Ni они равны соответственно 2,218; 1,715 и 0,604 mБ).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

МАГНИТНЫЙ МОМЕНТ

- физ. величина, характеризующая магн. свойства системы заряж. частиц (или отд. частицы) и определяющая наряду с др. мультипольными моментами (дипольным электрич. моментом, квадрупольным моментом и т. д., см. Мулътиполи )взаимодействие системы с внеш. эл.-магн. полями и с др. подобными системами.

Согласно представлениям классич. электродинамики, магн. поле создаётся движущимися электрич. зарядами. Хотя совр. теория не отвергает (и даже предсказывает) существование частиц с магн. зарядом ( магнитных монополей), такие частицы пока экспериментально не наблюдались и в обычном веществе отсутствуют. Поэтому элементарной характеристикой магн. свойств оказывается именно М. м. Система, обладающая М. м. 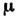(аксиальный вектор), на больших расстояниях от системы создаёт магн. поле

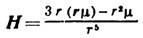
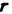(- радиус-вектор точки наблюдения). Аналогичный вид имеет электрич. поле диполя, состоящего из двух близко расположенных электрич. зарядов противоположного знака. Однако, в отличие от электрич. дипольного момента. М. м. создаётся не системой точечных "магн. зарядов", а электрич. токами, текущими внутри системы. Если замкнутый электрич. ток плотности 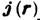течёт в ограниченном объёме V, то создаваемый им М. м. определяется ф-лой

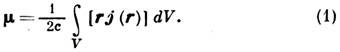
В простейшем случае замкнутого кругового тока I, текущего вдоль плоского витка площади s, 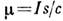, причём вектор М. м. направлен вдоль правой нормали к витку.

Если ток создаётся стационарным движением точечных электрич. зарядов 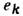с массами 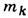, имеющими скорости 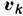, то возникающий М. м., как следует из ф-лы (1), имеет вид

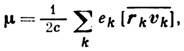
где подразумевается усреднение микроскопич. величин по времени. Поскольку стоящее в правой части векторное произведение пропорционально вектору момента кол-ва движения частицы 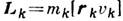(предполагается, что скорости 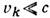), то вклады отд. частиц в М. м. и в момент кол-ва движения оказываются пропорциональными:

Коэффициент пропорциональности е/2тс наз. гиромагнитным отношением; эта величина характеризует универсальную связь между магн. и механич. свойствами заряж. частиц в классич. электродинамике. Однако движение элементарных носителей заряда в веществе (электронов) подчиняется законам квантовой механики, вносящей коррективы в классич. картину. Помимо орбитального механич. момента кол-ва движения L электрон обладает внутренним механич. моментом - спином 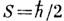. Полный М. м. электрона равен сумме орбитального М. м. (2) и спинового М. м.

Как видно из этой ф-лы (вытекающей из релятивистского Дирака уравнения для электрона), гиромагн. отношение для спина оказывается ровно в два раза больше, чем для орбитального момента. Особенностью квантового представления о магн. и механич. моментах является также то, что векторы 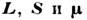не могут иметь определённого направления в пространстве вследствие некоммутативности операторов проекции этих векторов на оси координат.

Спиновый М. м. заряж. частицы, определяемый ф-лой (3), наз. нормальным, для электрона он равен магнетону Бора . Опыт показывает, однако, что М. м. электрона 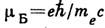отличается от (3) на величину порядка 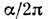( 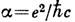- постоянная тонкой структуры). Подобная добавка, называемая аномальным магнитным моментом, возникает вследствие взаимодействия электрона с фотонами, она описывается в рамках квантовой электродинамики. Аномальными М. м. обладают и др. элементарные частицы; особенно велики они для адронов, к-рые, согласно совр. представлениям, имеют внутр. структуру. Так, аномальный М. м. протона в 2,79 раза больше "нормального" - ядерного магнетона, 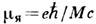( М - масса протона), а М. м. нейтрона равен -1,91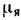, т. е. существенно отличен от нуля, хотя нейтрон не обладает электрич. зарядом. Такие большие аномальные М. м. адронов обусловлены внутр. движением входящих в их состав заряж. кварков.

Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; Xуанг К., Кварки, лептоны и калибровочные поля, пер. с англ., М., 1985. Д. В. Гилъцов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.