КОНТАКТНЫЕ НАПРЯЖЕНИЯ

КОНТАКТНЫЕ НАПРЯЖЕНИЯ

       

напряжения, к-рые возникают при механич. взаимодействии тв. деформируемых тел на площадках соприкосновения тел и вблизи них (напр., при сжатии соприкасающихся тел).

Распределение напряжений при сжатии сферич. тел: Р — сжимающая сила; p0 — макс. напряжение в центре площадки контакта; p — напряжение на расстоянии r от центра; а — радиус площадки; А — точка, в к-рой напряжение максимально.

Знание К. н. важно для расчёта на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрич. катков, соударяющихся тел и т. п. Размер поверхности контакта часто мал по сравнению с размерами тел, причём К. н. быстро убывают при удалении от места контакта. Распределение К. н. по площадке контакта (рис.) и в её окрестности неравномерно, причём макс. касат. напряжения, к-рые в значит. мере предопределяют прочность сжимаемых тел, возникают на нек-ром удалении (точка А) от площадки контакта.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

КОНТАКТНЫЕ НАПРЯЖЕНИЯ

механические - напряжения, к-рые возникают при механич. взаимодействии твёрдых деформируемых тел на площадках их соприкасания и вблизи площадок (напр., при сжатии соприкасающихся тел). Знание К. н. важно для расчёта на прочность подшипников, зубчатых и червячных передач, шариковых и цилиндрич. катков, кулачковых механизмов и т. п. Определение К. н. составляет задачу, наз. контактной.

Решение нек-рых контактных задач для упругих тел впервые дано Г. Герцем (G. Hertz). В основу его теории К. н. положены след, предположения: материал соприкасающихся тел в зоне контакта однороден и следует закону Гука; линейные размеры площадки контакта малы по сравнению с радиусом кривизны и линейными размерами соприкасающихся поверхностей в окрестности точек контакта; силы трения между соприкасающимися телами пренебрежимо малы. При этом найдено, что при сжатии двух тел, ограниченных плавными поверхностями, площадка контакта имеет форму эллипса (в частности, круга или полоски), а интенсивность распределения К. н. по этой площадке следует эллипсоидальному закону.

К. н. имеют местный характер, т. е. быстро убывают при достаточном удалении от места контакта (соприкасания тел). Распределение К. н. по площадке контакта и в её окрестности неравномерно и характеризуется большими градиентами. Важной особенностью распределения К. н. (напр., при сжатии шаров или пересекающихся цилиндров) является то, что макс, касательные напряжения 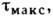к-рые в значит. мере предопределяют прочность сжимаемых тел, имеют место на нек-рой глубине под площадкой контакта. Вблизи самой этой площадки напряжённое состояние близко к гидростатич. сжатию, при к-ром, как известно, касательные напряжения отсутствуют.

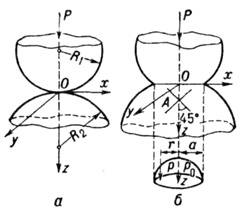
Рис. 1. Возникновение контактных напряжений при соприкосновении шаров.

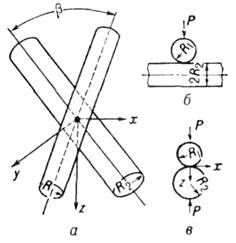
Рис. 2. Возникновение контактных напряжений при соприкосновении цилиндров.

Характерными случаями соприкасания упругих тел являются следующие.

1) Соприкасание шаров (рис. 1); площадка контакта имеет форму круга радиуса а, на к-ром действует давление с интенсивностью

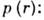
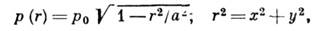
где

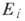(i = l, 2) - модуль Юнга материала рассматриваемых тел,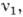 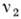- коэф. Пуассона, Р - равнодействующая сил, приложенных к каждому из соприкасающихся шаров, R₁ и R₂ - радиусы кривизн соприкасающихся поверхностей. Наибольшие сжимающие К. н. (рис. 1, б) действуют в центре площадки и равны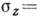 а между напряжениями 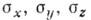в центре площадки контакта существует зависимость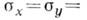 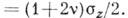Макс. касательные напряжения в этом случае равны 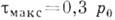и имеют место в точке А, отстоящей от центра площадки контакта по оси 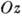на расстоянии 0,786 а.

2) Соприкасание двух цилиндров (рис. 2), оси к-рых образуют угол 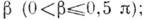площадка контакта - эллипс; интенсивность распределения давления по этой площадке определяется ф-лой

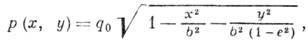
где

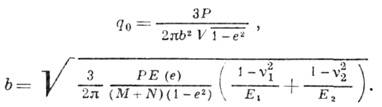
Эксцентриситет эллипса е определяется из соотношения

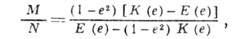
где

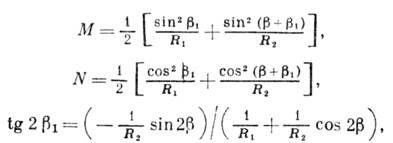
К(е), Е(е) - полные эллиптич. интегралы 1-го и 2-го рода.

Если угол 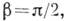а R₁=R₂ (рис. 2, б), то площадка контакта будет кругом и закон распределения давления по ней будет таким же, как и в случае сжатия шаров. Характерно, что макс. К. н. 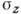при сжатии двух шаров радиуса R примерно в 1,6 раза больше макс. К. н. 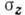при сжатии двух накрест лежащих цилиндров 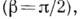радиусы к-рых равны R, а материал и равнодействующая Р такие же, как и у шаров.

Если 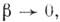то большая ось площадки контакта между соприкасающимися цилиндрами увеличивается и при 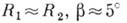(или при 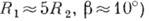становится сравнимой с радиусом цилиндра. В этом случае ф-лы для определения деформаций, полученные в теории Герца, не применимы. Однако ф-лы, полученные на основании этой теории (когда область контакта мала), имеют смысл и в этом случае, т. е. при 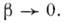В случае 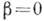(рис. 2, в )площадка контакта имеет вид полоски шириной 2l. Распределение давления по этой полоске определяется ф-лой

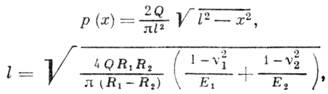
где Q - нагрузка на единицу длины цилиндра.

Теория Герца и проблема К. н. в целом получили значительное матем. развитие в течение последних двух-трёх десятилетий, что позволило изучить влияние сил трения между соприкасающимися телами на величину К. н.; исследовать случаи соприкасания тел, когда одно из них является гибким, напр. плиты и балки на упругом основании, подкрепляющие кольца и стержни; рассмотреть случаи, когда линейные размеры области контакта сравнимы с радиусом кривизны соприкасающихся тел, напр. давление цилиндра на край цилиндрич. отверстия в упругом теле, радиусы к-рых почти равны; решена задача в общем случае о давлении абсолютно жёсткого тела (штампа), круглого в плане, на упругое полупространство; решены нек-рые конкретные задачи для анизотропных тел и ряд др. задач.

Лит.: Рвачев В. Л., Проценко B. C., Контактные задачи теории упругости для неклассических областей, К., 1977; Моссаковский В. И., Гудрамович В. С., Макеев Е. М., Контактные задачи по теории оболочек и стержней, М., 1978; Галин Л. А., Контактные задачи теории упругости и вязкоупругости, М., 1980; Попов Г. Я., Концентрация упругих напряжений возле штампов, разрезов, тонких включений и подкреплений, М., 1982; Александров В. М., Мхитарян С. М., Контактные задачи для тел с тонкими покрытиями и прослойками, М., 1983; Теплый М. И., Контактные задачи для областей с круговыми границами, Львов, 1983. В. В. Панасюк.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.