НЕТЕР ТЕОРЕМА

НЕТЕР ТЕОРЕМА

       

фундаментальная теорема физики, устанавливающая связь между св-вамн симметрии физ. системы и сохранения законами. Сформулирована нем. математиком Э. Нётер (Е. Noether) в 1918. Н. т. утверждает, что для физ. системы, ур-ния движения к-рой имеют форму системы дифф. ур-ний и могут быть получены из вариационного принципа механики, каждому непрерывно зависящему от одного параметра преобразованию, оставляющему инвариантным действие (S), соответствует закон сохранения. Из условия обращения в нуль вариации действия, dS=0 (наименьшего действия принцип), получаются ур-ния движения системы. Каждому преобразованию, при к-ром действие не меняется, соответствует дифф. закон сохранения. Интегрирование ур-ния, выражающего такой закон, приводит к интегральному закону сохранения. Н. т. даёт наиб. простой и универсальный метод получения законов сохранения в классич. и квант. механике, в теории полей и т. д.

Непрерывными преобразованиями в пространстве-времени, оставляющими инвариантным действие (а следовательно, и ур-ния движения), являются: сдвиг во времени и в пр-ве, трёхмерное вращение, Лоренца преобразования. Согласно Н. т., из инвариантности относительно сдвига во времени следует закон сохранения энергии, относительно пространств. сдвигов — закон сохранения импульса, относительно пространств. вращения — закон сохранения момента кол-ва движения, относительно преобразований Лоренца — закон сохранения лоренцева момента, или обобщённый закон движения центра масс системы (центр масс релятив. системы движется равномерно и прямолинейно).

Н. т. относится не только к пространственно-временным симметриям. Так, из независимости динамики заряж. ч-ц в эл.-магн. полях от калибровочных преобразований (см. КАЛИБРОВОЧНАЯ СИММЕТРИЯ) следует закон сохранения заряда. Особенно важное значение Н. т. имеет в квант. теории поля, где законы сохранения, вытекающие из наличия определённой группы симметрии, явл. существ. источником информации о св-вах изучаемых объектов.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

НЁТЕР ТЕОРЕМА

- утверждает, <что для всякой физ. системы, уравнения движения к-рой могут быть полученыиз вариац. принципа, каждому однопараметрич. непрерывному преобразованию, <оставляющему вариац. функционал инвариантным, отвечает один дифференц. сохранениязакон, и, главное, позволяет явно выписать сохраняющуюся величину. <Установлена в работах учёных гёттингенской школы Д. Гильберта (D. Hilbert),Ф. Клейна (F. Klein) и Э. Нётер (Е. Noether). H. т. - самое универсальноесредство, позволяющее находить законы сохранения в лагранжевой классич. <механике, теории поля, квантовой теории и т. д.
В классич. механике для системы с действием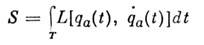

(L - Лагранжа функция, зависящаяот обобщённых координат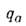 и скоростей 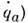инвариантность . относительнообразующих группу преобразовании с параметром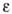

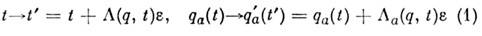
[где задающие преобразование ф-ции 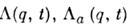зависят от совокупности координат 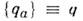ивремени] влечёт за собой, согласно Н. т., сохранение во времени величины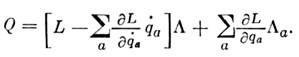

В частности, из инвариантности S относительно(1) с 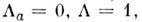т. е. из однородности времени, следует закон сохранения энергии: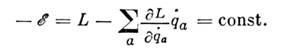

В этом случае L не зависит от времениявно. Подобным же образом из инвариантности S по отношению к пространств. <сдвигам 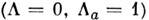следует закон сохранения импульса, а из изотропии пространства - законсохранения трёхмерного момента.
В гамильтоновом описании, т. е. когдаQвыражены через канонические переменные - обобщённые координатыи импульсы (для простоты считаем, что явные зависимости от времени отсутствуют):1) Пуассона скобкаQс гамильтонианом и равна нулю,2) изменение любой динамич. переменной F при преобразовании (1)определяется её скобкой Пуассона с Q.В этом контексте утверждениеН. т. становится как бы тривиальным, следующим из одной лишь антисимметриискобок Пуассона: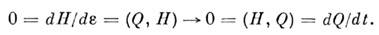

Если преобразования симметрии образуютне однопараметрич. группу, то между Q_A должны выполнятьсясоотношения в скобках Пуассона, воспроизводящие Ли алгебру генераторовсоответствующей группы. Так, напр., три компоненты момента должны удовлетворятьсоотношению в скобках Пуассона

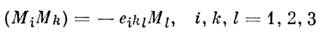
(где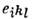 - Леви - Чивиты символ), воспроизводящему алгебру Ли группы трёхмерныхвращений 0(3).
Особо важное значение Н. т. приобретаетв квантовой теории поля (КТП), где вытекающие из наличия группысимметрии законы сохранения часто оказываются единств. источником информациио свойствах системы. Для формального вывода Н. т. в (классич. или квантовой)теории поля рассматривают интеграл действия: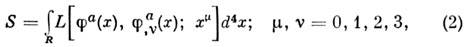

где 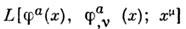- лагранжиан, зависящий от ф-ций поля 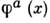,их первых производных по всем четырём координатам 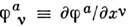и, возможно, от координат 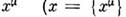- точка пространства-времени; индекс а нумерует компоненты поля;принята система отсчёта, в к-рой 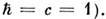Тогда Н. т. утверждает, что из инвариантности действия (2) относительнопреобразований с параметрами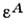

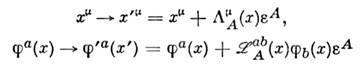
для произвольной области интегрирования . вытекаетдпфференц. закон сохранения:

где т. н. нётеров ток 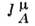вычисляется из лагранжиана по правилу: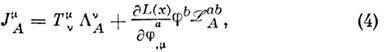

где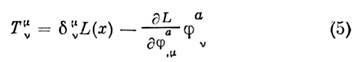

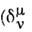- символ Кронекера; по повторяющемуся индексу предполагается суммирование).Интегрируя (3) по произвольному 4-объёму и используя Гаусса теорему, получаем, <что полный 4-поток вектора 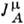через ограничивающую этот объём гиперповерхность равен нулю. Выбирая гиперповерхностьв виде цилиндра с пространственноподобными основаниями, такого, что потокомчерез боковые стенки можно пренебречь, приходим к утверждению, что направленныев будущее потоки вектора 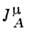черезнижнее и верхнее основания равны. Отсюда следует, что нётеровы заряды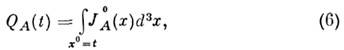

во-первых, сохраняются во времени (интегральнаяформа Н. т.), во-вторых, преобразуются при Лоренца преобразованиях контравариантносоответствующим параметрам
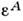
Из физ. представлений об однородностии изотропии пространства-времени следует, что для любой замкнутой системыдействие должно быть инвариантно относительно преобразований Пуанкарегруппы, что в силу Н. т. приводит к существованию 10 фундаментальныхсохраняющихся величин: энергии, трёх компонент импульса и 6 компонент 4-момента. <Сохранение энергии и импульса следует из инвариантности относительно трансляций . При этом 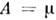,,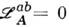 нётеровы токи исчерпываются выражением (5) и образуют тензор энергии-импульса. <Сохраняющиеся "заряды" суть компоненты 4-импульса: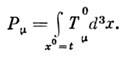

Из инвариантности относительно трёх пространств. <поворотов и трёх преобразований Лоренца

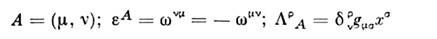
(где 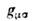- метрический тензор )вытекает дифференц. закон сохранения для тензораплотности момента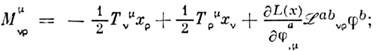

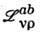определяется спином полей. Соответствующий нётеров заряд есть 4-момент.
В гамильтоновом описании 10 фундам. величинявляются генераторами соответствующих преобразований группы Пуанкаре иобразуют относительно скобок Пуассона замкнутую алгебру Ли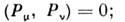

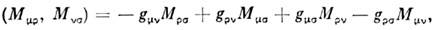
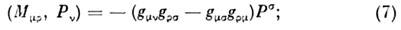
изоморфную алгебре Ли группы Пуанкаре. <Требование выполнения соотношений (7) в гамильтоновом формализме эквивалентнотребованию инвариантности лагранжиана относительно группы Пуанкаре в лагранжевомформализме.
При наличии в системе симметрии, не связанныхс пространством-временем ( внутренних симметрии), Н. т. позволяетпостроить и другие сохраняющиеся величины. При этом в выражении (4) длянётерова тока остаётся только второй член. Напр., если в системе с комплекснымполем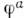 действиеинвариантно относительно глобального (с фазой 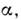не зависящей от х )калибровочного преобразования 1-го рода
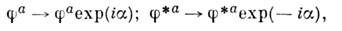тобудут сохраняться ток 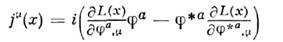исоответствующий заряд. В построении совр. реалистич. квантовополевых моделейтоки и заряды, сохраняющиеся в силу инвариантности относительно достаточносложных калибровочных групп, играют ведущую роль. Выражение (4) для пространственно-временнойлокализации нётерова тока (это выражение наз. каноническим) не однозначно, <если исходить только из требования выполнения дифференц. закона сохранения(З)и получения правильной интегральной величины (6).

Выполнение этих требований не нарушаетсяпри замене

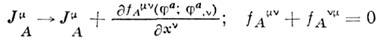спроизвольной ф-цией f. Этим произволом пользуются, чтобы заменитьканонич. тензор 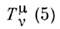(не симметричный для отличного от нуля спипа) на симметричный (тензор Белинфанте),выбирая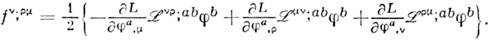

Для нулевого спина то же преобразованиепозволяет получить для безмассового поля 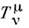снулевым следом.
Однозначные выражения для нётеровых токовполучаются варьированием по полям, для к-рых эти токи служат источниками.
Для теорий, обладающих суперсимметрией, независимымипеременными при выводе Н. т. будут наряду с х и антикоммутирующнекоординаты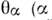 - спинорный индекс). Это приводит к обобщению фундам. сохраняющихся величин, <а также к появлению новых сохраняющихся величин: спин-векторных токов исоответствующих им суперзарядов, образующих представление супералгебрыПуанкаре.
Для классич. теории поля выписанных формальныхвыражений вполне достаточно. В квантовой теории поля выражения (4), (6),как правило, нуждаются в регуляризации (см. Регуляризация расходимостей )и перенормировке. Приэтом может оказаться, что формально имеющаяся симметрия не может быть сохраненадля регуляризов. выражений, и соответствующий закон сохранения перестаётвыполняться - говорят, что присутствует аномалия. Так, при рассмотрениивзаимодействия безмассовых фермпонов с эл.-магн. полем в классич. теориинаряду с векторным сохраняется также и аксиальный ток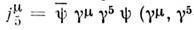 - Дирака матрицы). В квантовой теории во втором порядке по заряду . возникаетаномалия, и вместо сохранения тока получаем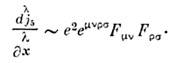

Вторая теоремаНётер. Помимообсуждавшейся выше Н. т., к-рую принято называть первой Н. т., существуетвторая Н. т., к-рая касается тождеств, вытекающих из инвариантности действияотносительно преобразований, зависящих от непрерывного параметра, т. е. <от произвольной ф-ции. Наиб. значение она получает в применении к случаю"полей материи", взаимодействующих с калибровочным полем А(х) - полем, <физ. содержание к-рого не меняется при определённых, зависящих от произвольнойф-ции 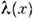преобразованиях, называемых преобразованиями калибровки. Вычисляя вариациюдействия для поля материи во внеш. калибровочном поле, вызванную бесконечномалым калибровочным преобразованием 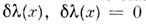на границах области интегрирования, следует учитывать только вызываемыеизменением калибровки вариации калибровочного поля 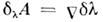(здесь 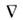- ковариантная производная), поскольку при вариациях полей материи коэффициентамибудут левые части ур-ний движения. Поэтому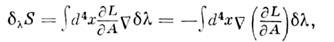

откуда в силу произвольности 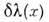вытекает ковариантный закон сохранения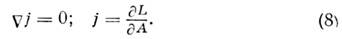

При обращении в ф-ле (8) внеш. калибровочногополя в нуль ковариантный закон сохранения превращается в обычный, получаемыйпо первой Н. т. Подчеркнём, что вторая Н. т. приводит к ограничениям наполя материи, исходя из особенностей калибровочного поля. Т. о., она устанавливаетсоответствие между свойствами материальных систем и полей, с к-рыми онимогут взаимодействовать. Поскольку в правых частях ур-ний движения самихкалибровочных полей стоят как раз токи (8), то вторая Н. т. налагает тождеств. <соотношения на левые части этих ур-ний. В совр. квантовой теории поля втораяН. т. используется в электродинамике, теории Янга - Миллса полей, гравитации, супергравитации ит. д.

Лит.:Hilbert D., Die Grundlagender Physik, "Gott. Nachr., Math. Phys. Klassc", 1915, S. 395; Klein F.,Die Differentialgeselze fur die Erhaltung von Impuls und Energie in derEinsteinsch. Gravitatioristheorie, там же, 1918, S. 171; Nоther Е., InvarianteVariationsprobleme, там же, 1918, S. 235; Ландау Л. Д., Лифшиц Е. М., Теорияполя, 7 изд., М., 1988; Паули В., Релятивистская теория элементарных частиц, <пер. с англ., М., 1947; Боголюбов Н. Н., Ширков Д. В., Введение в теориюквантованных полей, 4 изд., М., 1984; Гельфанд И. М., Фомин С. В., Вариационноеисчисление, М., 1961; Медведев Б. В., Начала теоретической физики, М.,1977.

Б. В. Медведев, П. Б. Медведев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.