ВЕЕРНОЕ ПРОИЗВЕДЕНИЕ

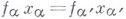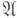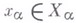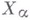системы топологических пространств относительно системы непрерывных отображений - подмножество тихоновского произведения., рассматриваемое в индуцированной топологии и состоящее из таких точек , для к-рых при любом выборе индексов и из . Отображение, ставящее в соответствие точке точку (соответственно точку , наз. проекцией В. п. в , (соответственно в ).

Если пространство одноточечно, то Если 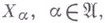- вполне регулярные пространства, то В. п. 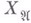вполне регулярно. В. п., и особенно их частный случай - частичное произведение, хорошо приспособлено к построению универсальных (в смысле гомеоморфного вложения) топологич. пространств данного веса и данной размерности (см. Универсальное пространство). Б. А. Пасынков.