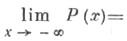ФУРЬЕ - СТИЛТЬЕСА ПРЕОБРАЗОВАНИЕ
- ФУРЬЕ - СТИЛТЬЕСА ПРЕОБРАЗОВАНИЕ
- одно из интегральных преобразований, родственное Фурье преобразованию. Пусть функция F(х)имеет ограниченное изменение на  Функция
Функция

наз. преобразованием Фурье - Стилтьеса для F. Функция 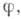 определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция
определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция 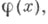 разлагающаяся в ряд Фурье
разлагающаяся в ряд Фурье  с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с
с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с 
Формула (*) допускает обращение: если F(х)имеет ограниченное изменение и

то
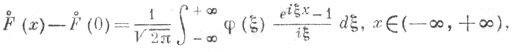
где интеграл понимается в смысле главного значения на 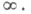
Если в формуле (*) в качестве функции F(х)допустить лишь неубывающие функции ограниченной вариации, то совокупность получающихся непрерывных функций 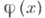 полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
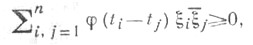
каковы бы ни были комплексные числа  (теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию
(теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию

подчиняют дополнительным ограничениям
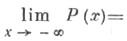

непрерывна слева, и именуют распределением, функцию

- характеристической функцией [распределения Р(х)].Теорема Бохнера-Хинчина выражает тогда необходимое и достаточное условие того, что непрерывная функция Ф(х)[для к-рой Ф(0)=1] является характеристической функцией нек-рого распределения.
Теория Ф.-С. п. развита и в n-мерном случае.
Лит.:[1] Бохнер С., Лекции об интегралах Фурье, пер. с англ., М., 1962; [2] Зигмунд А., Тригонометрические ряды, пер. с англ.. т. 2, М., 1965; [3] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.
П. И. Лизоркин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ФУРЬЕ - СТИЛТЬЕСА ПРЕОБРАЗОВАНИЕ" в других словарях:
Фурье преобразование — (данной функции) функция, выражающаяся через данную функцию f (x) формулой: Если функция f (x) чётная, то её ф. п. равно (косинус преобразование), а если f (x) нечётная функция, то … … Большая советская энциклопедия
ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ — функциональное преобразование вида где С конечный или бесконечный контур в комплексной плоскости, К( х, t) ядро И. п. Наиболее часто рассматриваются И. п., для которых K(x,t)=K(xt )и С действительная ось или ее часть ( а, b). Если то И. п. наз.… … Математическая энциклопедия
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ — преобразование Фурье Стилтьеса вероятностной меры комплскснозначная функция, заданная на всей числовой оси формулой X. ф. случайной величины Xпо определению есть X. ф. ее вероятностного распределения Метод, связанный с использованием X. ф., был… … Математическая энциклопедия
АЛГЕБРА МЕР — алгебра М(G).комплексных регулярных борелевских мер на локально компактной абелевой группе G, имеющих ограниченную вариацию, с обычными линейными операциями и сверткой в качестве умножения (см. Гармонический анализ абстрактный). Свертка полностью … Математическая энциклопедия
ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия
Функциональный анализ — I Функциональный анализ часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание… … Большая советская энциклопедия
Функциональный анализ (математ.) — Функциональный анализ, часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание методов… … Большая советская энциклопедия
 Функция
Функция 
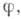 определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция
определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция 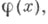 разлагающаяся в ряд Фурье
разлагающаяся в ряд Фурье  с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с
с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с 

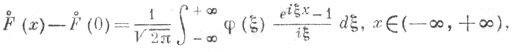
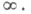
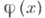 полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство 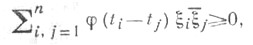
 (теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию
(теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию