ФЛОКЕ ТЕОРИЯ

- теория о строении пространства решений и о свойствах самих решений линейной системы дифференциальных уравнений с периодическими коэффициентами

матрица A(t)периодическая по . с периодом 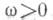и суммируемая на каждом компактном интервале из
1) Любая фундаментальная матрица . системы (1) имеет представление

наз. представлением Флокe (см. [1]), где F(t) - нек-рая -периодич. матрица, К - нек-рая постоянная матрица. Существует базис х ₁,...,х _n пространства решений системы (1) такой, что в этом базисе матрица . имеет жорданову форму; этот базис можно представить в виде
где -многочлены относительно t с 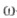-периодич. коэффициентами, - характеристические показатели системы (1). Любая компонента решения системы (1) является линейной комбинацией функций вида (решений Флоке) В случае когда все характеристич. показатели различны (или среди них есть кратные, но им отвечают простые элементарные делители), функции 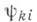суть просто -периодич. функции. В представлении (2) матрицы F(t)и К, вообще говоря, комплекснозначны. Если ограничиться только действительным случаем, то F(t) может не быть 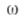-периодической, но обязательно будет 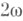-периодической.
2) Систему (1) можно привести к дифференциальному уравнению с постоянной матрицей у'=Ку с помощью преобразования Ляпунова

где F(t)и K -матрицы из представления Флоке (2) (см. [2]). Представление (2) вместе с подстановкой (3) часто называют теоремой Флоке - Ляпунова.
3) Пусть -спектр матрицы К. Для каждого такого, что 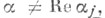_ j=1,..,l, в силу представления (2) пространство 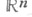распадается в прямую сумму двух подпространств 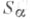и

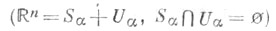
таких, что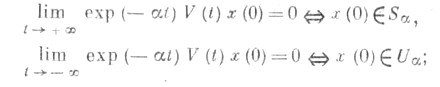
здесь V(t)-нормированная в нуле фундаментальная матрица системы (1). Отсюда следует экспоненциальная дихотомия системы (1), если
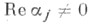ни для какого j= 1,...,l.

Лит.:[1] F1оquet G., лAnn. sci. Ecoie norm, super.