УПОРЯДОЧЕННЫЙ ГРУППОИД

группоид Н, множество элементов к-рого частично упорядочено отношением 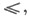и, кроме того, операция и порядок связаны аксиомой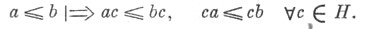

Если У . г . Н подчиняется более сильной аксиоме

то порядок в H наз. строгим, а Н - строгим частично упорядоченным группоидом. Частично У. г. наз. сильным, если

Сильный частично У. г. всегда является строгим, а для линейно У. г. эти два понятия совпадают.
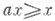Элемент аУ. г. Нназ. положительным (строго положительны м), если для всех справедливы неравенства и 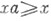(соответственно, ах>х и ха>х). Отрицательные и строго отрицательные элементы определяются двойственными неравенствами. У. г. наз. положительно (отрицательно) упорядоченным, если все его элементы положительны (отрицательны). Интерес для изучения представляют специальные типы группоидов (см. Естественно упорядоченный группоид, Упорядоченная . полугруппа, Упорядоченная группа).

О. А. Иванова.