- ТОПОЛОГИЧЕСКАЯ ЭНТРОПИЯ
понятие топологической динамики и эрзодической теории, аналогичное метрич. энтропии динамич. систем (введена в [1]). Для открытого покрытия
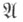компакта Xчерез 
обозначается логарифм (обычно двоичный) наименьшего числа элементов покрытия, к-рые все еще покрывают X. Если 
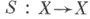- непрерывное отображение, то существует предел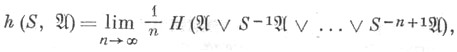 
где
- покрытие, элементы к-рого суть непустые пересечения элементов покрытий 
и 
Т. э.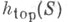 
определяют как верхнюю грань 
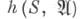по всевозможным 
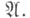Эквивалентное определение в ме-тризуемом случае: пусть для метрики 
через 
обозначено наибольшее число точек X, попарные расстояния между к-рыми больше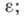 
тогда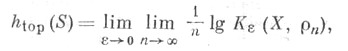 
где
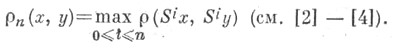
Оказывается, что
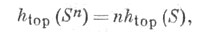
а если S - гомеоморфизм, то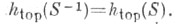
Поэтому Т. э. каскада{Sn}естественно считать 
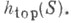Для топологич. потока{St}оказывается, что 
поэтому Т. э. потока естественно считать
Несколько иначе определяется Т. э. для других групп преобразований (она уже не сводится к Т. э. одного из преобразований, входящих в группу; см [7]).
Т. э.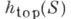
совпадает с верхней гранью метрич. энтропии 
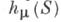по всевозможным нормированным борелевским инвариантным мерам 
(см. [2], [5] - [7]). Это - частный случай вариационного принципа, устанавливающего топологич. интерпретацию величины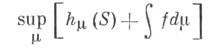 
с фиксированной непрерывной функцией f (см. [4], [8], [9]). Т. э. дает характеристику лсложности
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
