- СЛОЕНИЕ
на n-мерном многообразии М n - такое разбиение М n на линейно связные подмножества, именуемые слоями, что М n можно покрыть координатными окрестностями Ua с локальными координатами
 , в терминах к-рых локальные слои - компоненты связности пересечения слоев с Ua, задаются уравнениями
, в терминах к-рых локальные слои - компоненты связности пересечения слоев с Ua, задаются уравнениями  =
= . С. в этом смысле наз. топологическим С.; требуя же, чтобы М п имело кусочно линейную, дифференцируемую или аналитич. структуру и чтобы локальные координаты были кусочно линейными, дифференцируемыми (класса С r). или аналитическими, получают определение кусочно линейного, дифференцируемого (класса С r).или аналитического С. Определение дифференцируемого С. класса С r формально годится и при r=0, совпадая в этом случае с определением топологич. С. Обычно, говоря о дифференцируемом С., подразумевают, что
. С. в этом смысле наз. топологическим С.; требуя же, чтобы М п имело кусочно линейную, дифференцируемую или аналитич. структуру и чтобы локальные координаты были кусочно линейными, дифференцируемыми (класса С r). или аналитическими, получают определение кусочно линейного, дифференцируемого (класса С r).или аналитического С. Определение дифференцируемого С. класса С r формально годится и при r=0, совпадая в этом случае с определением топологич. С. Обычно, говоря о дифференцируемом С., подразумевают, что  . Слои естественно снабжаются структурой n-мерных многообразий (топологических, кусочно линейных, дифференцируемых или аналитических) и тем самым оказываются подмногообразиями (в широком смысле слова) многообразия М п. Число р(размерность слоев) наз. размерностью С., a q=п-р - его коразмерностью. Рассматривая С. на многообразии с краем, обычно требуют либо трансверсальности слоев к краю, либо же того, чтобы слой, пересекающийся с краем, целиком в нем содержался. Очевидным образом определяются комплексно-аналитические С. Основным в теории С. является дифференцируемый случай (ниже С. и отображения, как правило, подразумеваются дифференцируемыми) .
. Слои естественно снабжаются структурой n-мерных многообразий (топологических, кусочно линейных, дифференцируемых или аналитических) и тем самым оказываются подмногообразиями (в широком смысле слова) многообразия М п. Число р(размерность слоев) наз. размерностью С., a q=п-р - его коразмерностью. Рассматривая С. на многообразии с краем, обычно требуют либо трансверсальности слоев к краю, либо же того, чтобы слой, пересекающийся с краем, целиком в нем содержался. Очевидным образом определяются комплексно-аналитические С. Основным в теории С. является дифференцируемый случай (ниже С. и отображения, как правило, подразумеваются дифференцируемыми) .
Отображение
 является субмерсией. Локальные слои суть
является субмерсией. Локальные слои суть  ,
,  .
.Система локальных субмерсий {(Ua, ja)} является согласованной в том смысле, что если
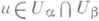 , то возле и можно перейти от ja(v). к jb(v) с помощью нек-рого локального диффеоморфизма
, то возле и можно перейти от ja(v). к jb(v) с помощью нек-рого локального диффеоморфизма 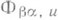 (класса С r).пространства
(класса С r).пространства  , т. е. для всех v, достаточно близких к и, имеет место
, т. е. для всех v, достаточно близких к и, имеет место  . Обратно, если М п покрыто областями Ua. и заданы субмерсий
. Обратно, если М п покрыто областями Ua. и заданы субмерсий  , согласованные в том же смысле, что и выше, то путем подходящего "склеивания"
, согласованные в том же смысле, что и выше, то путем подходящего "склеивания"  между собой получается такое С., что каждое
между собой получается такое С., что каждое 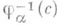 содержится в нек-ром слое.
содержится в нек-ром слое.
Сопоставление каждой точке
 касательного пространства к проходящему через эту точку слою, приводит к нек-рому полю р-мерных касательных подпространств (но другой терминологии, р-мерному расслоению), к-рое наз. касательным полем С. При р=1 любое поле p-мерных касательных подпространств, при самых минимальных требованиях дифференцируемостй, является касательным нолем нек-рого однозначно определенного С. При p>1 это не так. Данный вопрос имеет локальный характер (см. Фробениуса теорема).
касательного пространства к проходящему через эту точку слою, приводит к нек-рому полю р-мерных касательных подпространств (но другой терминологии, р-мерному расслоению), к-рое наз. касательным полем С. При р=1 любое поле p-мерных касательных подпространств, при самых минимальных требованиях дифференцируемостй, является касательным нолем нек-рого однозначно определенного С. При p>1 это не так. Данный вопрос имеет локальный характер (см. Фробениуса теорема).Непосредственное применение теоремы Фробениуса к инволютивному распределению показывает, что при выполнении соответствующих условий имеется система согласованных локальных субмерсий, для к-рых заданное поле касается, переход к С. осуществляется путем надлежащих "склеиваний" (в других терминах это описано в [3]).
Формирование понятия С. произошло в 40-х гг. 20 в. в цикле работ Ж. Риба (G. Reeb) и III. Эресмана (Ch. Ehresmann), завершившемся книгой [1] (в связи с историей см. [2]), и было связано с переходом к глобальной точке зрения. Этому отчасти способствовала теория гладких динамических систем, где разбиение фазового многообразия (с выкинутыми равновесия положениями).на траектории потока является одномерным С. Особое положение, к-рое в этой теории занимают потоки на поверхностях (Пуанкаре- Бендиксона теория, Дифференциальные уравнения на торе, Кнезера теорема). Особое положение, где траектории локально разбивают пространство, способствовало привлечению внимания к С. коразмерности 1. Другой пример С., проанализированный в 40-х гг.,- разбиение группы Ли на смежные классы по аналитич. одгруппе (не обязательно замкнутой) (см. [3]). Наконец, в комплексной области решения дифференциального уравнения dw/dz=f(z, w).с аналитической правой частью образуют (с вещественной точки зрения) двумерное С.
После первых работ наступил перерыв в развитии теории С., к-рая тогда была еще бедна значительными результатами. Интенсивное развитие началось с работ А. Хефлигера [4] и С. П. Новикова [7], наиболее известные результаты к-рых таковы (см. [17]): С. коразмерности 1 на трехмерной сфере имеет компактный слой [7] и не может быть аналитическим [4], хотя еще Ж. Риб построил С. класса
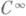 . Тогда же при изучении нек-рых динамич. систем (У-системы и родственные им) возникли нек-рые вспомогательные С. (уже не одномерные, что тоже стимулировало исследование С. (см. [7], [8]). Все эти работы и ряд последующих можно отнести к "геометрическому" или "качественному" направлению [16]. В нем большое внимание уделяется С. коразмерности 1, существованию компактных слоев, теоремам устойчивости (устанавливающим, что при определенных условиях С. с компактным слоем устроено в его окрестности и глобально как расслоение; первые такие теоремы доказал еще Ж. Риб, см. [17]), характеристике "роста" слоев (т. е. зависимости р-мерного объема геодезич. шара радиуса r на слое от r).или их фундаментальных групп. Отметим также недавнее решение вопроса: если на замкнутом М п имеется р-мерное С., все слои к-рого компактны, то обязательно ли ограничен р-мерный объем слоев? Д. Эпстейн (D. Epstein), Д. Сулливан (D. Sullivan) и др. выяснили, что ответ положительный только при
. Тогда же при изучении нек-рых динамич. систем (У-системы и родственные им) возникли нек-рые вспомогательные С. (уже не одномерные, что тоже стимулировало исследование С. (см. [7], [8]). Все эти работы и ряд последующих можно отнести к "геометрическому" или "качественному" направлению [16]. В нем большое внимание уделяется С. коразмерности 1, существованию компактных слоев, теоремам устойчивости (устанавливающим, что при определенных условиях С. с компактным слоем устроено в его окрестности и глобально как расслоение; первые такие теоремы доказал еще Ж. Риб, см. [17]), характеристике "роста" слоев (т. е. зависимости р-мерного объема геодезич. шара радиуса r на слое от r).или их фундаментальных групп. Отметим также недавнее решение вопроса: если на замкнутом М п имеется р-мерное С., все слои к-рого компактны, то обязательно ли ограничен р-мерный объем слоев? Д. Эпстейн (D. Epstein), Д. Сулливан (D. Sullivan) и др. выяснили, что ответ положительный только при  (см. [9]).
(см. [9]).
Позднее возникло "гомотопическое" направление, прообразом к-рого послужила гомотопич. теория расслоений. Отличия, возникающие для С., отчасти связаны с тем, что для С., вообще говоря, нет аналога индуцированному расслоению. Это вынуждает перейти от С. к более общим объектам - Хефлигера структурам (нечто вроде С. с особенностями), для к-рых такой аналог имеется.
Слоения F0 и F1 на Мназ. конкордантными, если на "цилиндре" МХ [0, 1] существует такое С. (той же коразмерности), слои к-рого трансверсальны ко "дну" и "крышке" цилиндра и "высекают" на них слоения F0 и F1. Сходным образом определяется конкордантность структур Хефлигера. Всякая структура Хефлигера конкордантна такой, к-рая вне множества "особых точек" на Мсоответствует нек-рому С., причем выполняются определенные условия о поведении слоев последнего возле этих точек. В этом смысле структуру Хефлигера можно представить себе как С. с особенностями. Имеется естественное биективное соответствие между классами конкордатных структур Хефлигера и гомотопич. классами непрерывных отображений М в т. <н. классифицирующее пространство
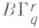 (q указывает коразмерность, r - класс гладкости структуры Хефлигера).
(q указывает коразмерность, r - класс гладкости структуры Хефлигера).
Гомотопич. теория устанавливает, какие гомотопич. объекты определяют конкордантность С.: два С. конкордантны тогда и только тогда, когда они конкордантны как структуры Хефлигера, а их касательные поля гомотопны (см. [6], |10], [11]). Родственный результат - доказательство существования р-мерных С. на любых открытых М(см. [6J) и на таких замкнутых М, на к-рых существует непрерывное поле р-мерных касательных подпространств (что является очевидным необходимым условием существования С., см. [10], [11]), ранее различными учеными было доказано существование С. на ряде многообразий путем непосредственных построений [12]. Идея (см. [10], [11]) состоит в том, чтобы, пачав со С. с особенностями, ликвидировать их путем нек-рых модификаций С. Случай q>1 оказывается более простым (см. [10], [13]) и ликвидация особенностей может быть проведена в духе "геометрической" теории [14]; случай q=1 сложнее [11].
Отображение порождает отображение когомологий, что
 приводит к характеристическим классам С. В возникающую здесь "гомологическую" или "количественную" теорию С. (см. [13], [15], [16]) включаются и нек-рые результаты, полученные ранее без обращения к
приводит к характеристическим классам С. В возникающую здесь "гомологическую" или "количественную" теорию С. (см. [13], [15], [16]) включаются и нек-рые результаты, полученные ранее без обращения к  , напр. инвариант Годбийона-Вея; для n=3 (см. [17]) или указанные P. Боттом (R, Bott( условия, необходимые для того, чтобы непрерывное поле касательных подпространств было гомотопно касательному полю С.
, напр. инвариант Годбийона-Вея; для n=3 (см. [17]) или указанные P. Боттом (R, Bott( условия, необходимые для того, чтобы непрерывное поле касательных подпространств было гомотопно касательному полю С.
Лит.: [1] Rееb G., в кн.: Actualites Sci. Ind.,№ 1183, P., 1952; [2] Reeb G., Schweitzer P. А., в кн.: Differential topology..., В., 1978; [3] Шевалле К., Теория групп Ли, пер. с англ., т. 1, М., 1948; [4] Haefliger A., "Ann. Scuola norm. Sup. Pisa", ser. 3, 1962, t. 16, p. 367-97; [5] его же, в кн.: Manifolds, Amst., 1970, В., 1971; [6] его же, "Topology", 1970, v. 9, № 2, р. 183-94; [7] Новиков С. П., "Тр. Моск. матем. об-ва", 1965, т. 14, с. 248-78; [8] Гладкие динамические системы, [пер.], М., 1977; [9] Бессе А., Многообразия с замкнутыми геодезическими, пер. с англ., М., 1981; [10] Тhurston W., "Comm. math. Helv.", 1974, v. 49, p. 214-31; [11] его же, ".Ann. Math.", 1976, v. 104, № 2, p. 249-68; [12] Lawsоn H., "Bull. Amer. Math. Soc.", 1974, v. 80, p. 369-418; [13] его же, The quantitative theory of foliations, Providence, 1977; [14] Мишачев H. М., Элиашберг Я. М., "Функц. анализ и его прил.", 1977, т. 11, № 3, с. 43-53; [15] Фукс Д. В., в кн.: Итоги науки и техн. Сер. Совр. пробл. матем., М., 1978, т. 10, с. 179-285; [16] его же, в кн.: Итоги науки и техн. Сер. Алгебра. Топология. Геометрия, М., 1981, т. 18, с. 151-213; [17] Тамура И., Топология слоений, пер. сяпон., М., 1979. Д. В. Аносов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
