РЕШЕТА МЕТОД

РЕШЕТА МЕТОД

- один из общих методов теории чисел, обобщающий принцип высеивания составных чисел из натурального ряда (см. Эратосфена решето). Проблема Р. м. состоит в оценке для конечного множества Ацелых чисел количества тех элементов, к-рые не делятся ни на какое простое число риз нек-рого множества Рпростых чисел. Оценивается "просеивающая" функция , обозначающая количество указанных элементов из Апри дополнительном условии: Для получения оценок просеивающей функции часто используется информация о числе элементов множества , состоящего из элементов А , к-рые делятся на свободное от квадратов число . При множество . Поэтому обычно оценивается более общая просеивающая функция

При выборе ожидаемого значения для 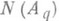в форме 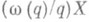, где X - ожидаемое значение для N (А)и 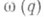- мультипликативная функция, руководствуются тем, чтобы погрешность


была относительно мала. Если при этом w(p)=k (по крайней мере, "в среднем"), то kназ. размерностью решета.

Общая теория Р. м. с ее приложениями продвинулась наиболее далеко в случае линейного решета (при k=1). Существуют различные специализации Р. м., наиболее важные из к-рых принадлежат В. Бруну (V. Brun; см. Бруна решето).и А. Сельбергу (A. Selberg; см. Селъ-берга решето).

В приложениях P.м. к аддитивным задачам (см. Аддитивная теория чисел), кроме оценок просеивающей функции сверху, необходимы оценки этой функции снизу. Получение оценок снизу может быть основано на логическом комбинаторном тождестве


Наиболее точные оценки снизу получаются с добавлением комбинаторных соображений, связанных с использованием весовых функций. Сильный результат в приложениях Р. м. с весовыми функциями состоит в том, что каждое достаточно большое четное число Nпредставимо в виде , где р - простое число, Р 2 содержит не более двух простых множителей.

Лит.:[1] П р а х а р К., Распределение простых чисел, пер. с нем., М., 1967; [2] Г е л ь ф о н д А. О., Л и н н и к Ю. В., Элементарные методы в аналитической теории чисел, М., 1962; [3] H a l b e r s t a m Н., R i c h e r t H., Sieve methods, L.- [а. о.], 1974. Б. М. Бредихин.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "РЕШЕТА МЕТОД" в других словарях:

  • Метод квадратичного решета — (Quadratic sieve algorithm, сокр. QS)  метод факторизации больших чисел, разработанный Померанцем в 1981 году. Долгое время превосходил другие методы факторизации целых чисел общего вида, не имеющих простых делителей, порядок которых… …   Википедия

  • Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… …   Википедия

  • Специальный метод решета числового поля — (англ. special number field sieve, SNFS) является методом факторизации целых чисел особого вида. Из него был получен общий метод решета числового поля, являющийся наиболее эффективным алогритмом факторизации больших целых чисел . Метод… …   Википедия

  • ДИСПЕРСИОННЫЙ МЕТОД — в теории чисел метод для решения нек рых бинарных уравнений (бинарных аддитивных проблем )вида где a и b принадлежат к достаточно густым и хорошо распределенным в арифметич. прогрессиях последовательностям натуральных чисел. Д. м., разработанный… …   Математическая энциклопедия

  • ПЛОТНОСТНЫЙ МЕТОД — один из методов аналитич. теории чисел, основанный на изучении статистики распределения нулей дзета функции Римана и L функции Дирихле s=s+it характер по модулю k. Многие теоретико числовые проблемы получают наиболее законченное решение в… …   Математическая энциклопедия

  • АДДИТИВНЫЕ ПРОБЛЕМЫ — проблемы теории чисел о разложении целых чисел на слагаемые заданного вида. Решение классич. А. п. привело к созданию новых методов в теории чисел. К классич. А. п. относятся: 1) Гольдбаха проблема о представлении нечетных натуральных чисел,… …   Математическая энциклопедия

  • СЕЛЬБЕРГА РЕШЕТО — С е л ь б е р г а м е т о д, специальный и в то же время достаточно универсальный решета метод, созданный А. Сельбергом [1]. С. р. позволяет хорошо оценивать сверху просеивающую функцию S(А; Р, z), обозначающую количество элементов конечного… …   Математическая энциклопедия

  • БРУНА РЕШЕТО — один из решета методов в элементарной теории чисел, созданный В. Вруном [1]; является развитием Эратосфена решета. Метод Б. р. заключается в следующем: из последовательности натуральных чисел высеиваются (выбрасываются) числа с малыми простыми… …   Математическая энциклопедия

  • ЭРАТОСФЕНА РЕШЕТО — метод, разработанный Эратосфеном (3 в. до н. э.) и позволяющий отсеивать составные числа из натурального ряда. Сущность Э. р. заключается в следующем. Зачеркивается единица. Число 2 простое. Зачеркиваются все натуральные числа, делящиеся на 2.… …   Математическая энциклопедия

  • RSA-числа — это множество больших полупростых чисел (чисел, представимых в виде произведения двух простых чисел), используемых в конкурсе RSA Factoring Challenge. Конкурс заключался в нахождении простых множителей предложенных чисел, но в 2007 году был… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»