- ПОВТОРНЫЙ ИНТЕГРАЛ
интеграл, в к-ром последовательно выполняется интегрирование по разным переменным, т. е. интеграл вида
 (1)
(1)
Функция f(x, y).определена на множестве А, лежащем в прямом произведении XX Y пространств Xи У, в к-рых заданы s-конечные меры mx и my, обладающие свойством полноты; множество
 ("сечение" множества А), измеримое относительно меры m х;. множество А у (проекция множества Ав пространство Y), измеримое относительно меры m у. Интегрирование по (у).производится по мере (mx, а по А у - по мере my. Интеграл (1) обозначают также
("сечение" множества А), измеримое относительно меры m х;. множество А у (проекция множества Ав пространство Y), измеримое относительно меры m у. Интегрирование по (у).производится по мере (mx, а по А у - по мере my. Интеграл (1) обозначают также
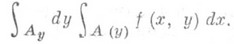
К П. и. могут быть сведены кратные интегралы. Пусть функция f(x, у), интегрируемая по мере
 на множестве
на множестве 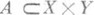 , продолжена нулем на все пространство
, продолжена нулем на все пространство 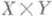 , тогда П. и.
, тогда П. и.
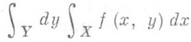
и
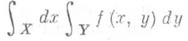
существуют и равны между собой:
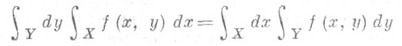 (2)
(2)
(см. Фубини теорема). В левом интеграле внешнее интегрирование фактически производится по множеству
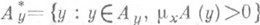 . Таким образом, в частности, для точек
. Таким образом, в частности, для точек  множества (у).измеримы относительно меры m х. По всему множеству А у брать этот интеграл, вообще говоря, нельзя, т. к. при измеримом относительно меры m множества Амножество А у может оказаться неизмеримым относительно меры my, так же, как и отдельные множества (у),
множества (у).измеримы относительно меры m х. По всему множеству А у брать этот интеграл, вообще говоря, нельзя, т. к. при измеримом относительно меры m множества Амножество А у может оказаться неизмеримым относительно меры my, так же, как и отдельные множества (у),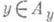 , могут быть неизмеримы относительно меры m х.
, могут быть неизмеримы относительно меры m х. Множество же
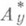 всегда измеримо относительно меры my, если только множество Аизмеримо относительно меры m.
всегда измеримо относительно меры my, если только множество Аизмеримо относительно меры m.
Сформулированные условия возможности перемены порядка интегрирования в П. и. являются лишь достаточными, но не необходимыми: иногда перемена порядка интегрирования в П. и. допустима, а соответствующий кратный интеграл не существует.
Напр., для функции
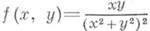 при x2+y2>0 и f(0, 0) = 0 П. и.
при x2+y2>0 и f(0, 0) = 0 П. и.
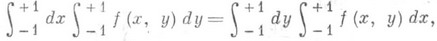
а кратный интеграл
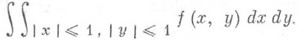
не существует. Однако если существует хотя бы один из интегралов
 или
или 
то функция f интегрируема на множестве
 и справедливо равенство (2).
и справедливо равенство (2).
Для П. и. в случае, когда внутренний интеграл является интегралом Стилтьеса, а внешний - интегралом Лебега, справедлива следующая теорема о перемене порядка интегрирования: пусть функция g(x, у). суммируема по уна [с, d]для всех значений хиз [ а, b]и является функцией ограниченной вариации по хна [ а, b]для почти всех значений
 . Пусть, далее, полная вариация функции g(x, у).но переменной хна [a, b]при всех указанных значениях уне превышает нек-рой неотрицательной и суммируемой на [с, d] функции. Тогда функция
. Пусть, далее, полная вариация функции g(x, у).но переменной хна [a, b]при всех указанных значениях уне превышает нек-рой неотрицательной и суммируемой на [с, d] функции. Тогда функция  является функцией ограниченной вариации от переменной хна [а, b]и для любой непрерывной на [а, b]функции f(х).имеет место формула
является функцией ограниченной вариации от переменной хна [а, b]и для любой непрерывной на [а, b]функции f(х).имеет место формула

Лит.:[1] Ильин В. А., Полняк Э. Г., Основы математического анализа, 2 изд., ч. 2, М., 1980; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [3] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [4] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975; [5] Смирнов В. И., Курс высшей математики, т. 5, М., 1959. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
