- ПИРСОВСКОЕ РАЗЛОЖЕНИЕ
представление кольца в виде прямой суммы подколец, связанное с данным идемпотентом е. Для кольца R, содержащего идемпотент е, существуют левое, правое и двустороннее П. р., определяемые равенствами

соответственно. При этом в случае отсутствия в Rединицы полагают, по определению,
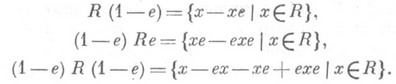
Множества (1-e)Rи eR(1-е).определяются аналогично. Таким образом, при двустороннем П. р. элемент
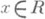 представляется в виде
представляется в виде

при левом - в виде

и при правом - в виде

Рассматривается также П. р. относительно ортогональной системы идемпотентов
 , где
, где 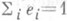 , а именно:
, а именно:

П. р. было предложено Б. Пирсом (см. [1]).
Лит.:[1] Реirсе В., "Amer. J. Math.", 1881, v. 4, p. 97.
Л. А. Скорняков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
