МОДУЛЯРНАЯ ГРУППА

- группа Г всех дробно-линейных преобразований 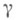вида

где 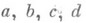- целые рациональные числа. М. г. отождествляется с факторгруппой

,

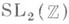и является дискретной подгруппой в группе Ли . Здесь (соответственно ) - группа матриц 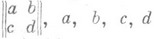- действительные (соответственноцелые) числа, М. г. является дискретной группой преобразований верхней комплексной полуплоскости (плоскости Лобачевского) и допускает представление образующими 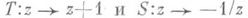и соотношениями , т. е. является свободным произведением циклич. группы порядка 2, порожденной S, и циклич. группы порядка 3, порожденной ST (см. [2]).

Интерес к М. г. связан с изучением модулярных функций, римановой поверхностью к-рых является фактор-пространство HIT, отождествляемое с фундаментальной областью GМ. г. Компактификация аналитически изоморфна комплексной проективной прямой, причем изоморфизм задается основной модулярной функцией 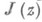. Фундаментальная область Gимеет конечную площадь Лобачевского

т. е. М. г. есть фуксова группа 1-го рода (см. [3]). Для решетки 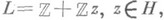решетка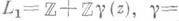 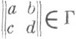, эквивалентна 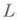, т. е. получается из умножением элементов последней на ненулевое комплексное число

Каждой решетке соответствует комплексный тор 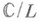, аналитически эквивалентный неособой кубич. кривой (эллиптич. кривой). Это дает взaимнooднoзначное соответствие между точками факторпространства , классами эквивалентных решеток и классами (аналитически) эквивалентных эллиптич. кривых (см. [3]).

Исследование подгруппы М. г. представляет интерес в теории модулярных форм и алгебраических кривых. Главной конгруэнц-подгруппой М. г. уровня 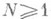(N - целое число) наз. группа преобразований вида (1), у к-рых 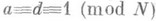, . Подгруппа наз. конгруэнцподгруппой, если для нек-рого числа N;наименьшее такое Nназ. уровнем 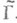Примеры конгруэнц-подгрупп уровня N:группа преобразований (1) с с, делящимся на N, группа 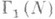преобразований (1) с и 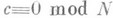. Индекс подгруппы в М. г. равен 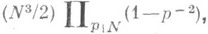если N>2, р - простые числа и 6, если N-2, поэтому каждая конгруэнцтподгруппа имеет конечный индекс в М. г.

Каждой подгруппе 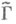конечного индекса в М. г. соответствует полная алгебраич. кривая ( модуляр ная кривая), полученная из факторпространства 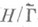, и накрытие . Изучение ветвления этого накрытия позволяет найти для конгруэнц-подгрупп Г образующие и соотношения, род кривой 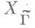и доказать, что существуют подгруппы конечного индекса в М. г., не являющиеся конгруэнц-подгруппами (см. [3], [8], [7] т. 2). Изучение представлений М. г. началось в работах (см. [4], [6]) в связи с теорией модулярных форм. Такие представления интенсивно изучаются в рамках теории автоморфных форм (см. [7]). Многие результаты, относящиеся к М. г., переносятся на случай арифметич. подгрупп в алгебраич. группах Ли.

Лит.:[1] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968: [2] Серр Ж.-П., Курс арифметики, пер. с франц., М., 1972; [3] Шимура Г., Введение в арифметическую теорию автоморфных функций, пер. с англ., М., 1973; [4] Неске Е., Mathematische Werke, 2 Aufl., Gott., 1970, S. 789- 918; to] Klein F., Fricke R., Vorlesungen ilber die Theorie der elliptischen Modulfunktionen, Bd 1-2, Lpz., 1890-92; [6] Kloosterman H. D., "Ann. Math.", 1946, v. 47, p. 317- 447; [7] Modular functions of one variable, [v.] 1-6, B.- Hdlb.- N. Y., 1973-77; [8] Rankin R., Modular forms and functions, Camb., 1977.

А. А. Панчишпин.