- МИНИМИЗИРУЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
последовательность элементов
 ,
,  , минимизирующая непрерывный функционал I[z],
, минимизирующая непрерывный функционал I[z], :
: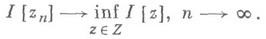
Задачи минимизации функционалов принято разделять на две группы. К первой относят нахождение минимального значения функционала, при к-ром несущественно, на каких элементах z достигается искомый минимум. В этом случае в качестве приближенных решений можно использовать значения функционала на любой М. п. Другая группа задач состоит в отыскании элемента
 , на к-ром функционал
, на к-ром функционал  достигает своего наименьшего значения:
достигает своего наименьшего значения:
При этом существуют М. п., не сходящиеся к элементу
 .
.Пусть задача минимизации (1) имеет единственное решение
 и
и  - М. п., т. е. такая последовательность, что
- М. п., т. е. такая последовательность, что
Задача минимизации (1) наз. устойчивой, если всякая М. п. (2) сходится к элементу

При решении устойчивых задач М. п. находится построением последовательности итераций таких, что по zn(n-й итерации) находится "направление" у п, а затем выбирается элемент

из множества элементов
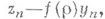 минимизирующих функцию
минимизирующих функцию  переменной
переменной  .
.Методы построения М. п. для устойчивых задач (1) распадаются на три семейства. В первом производные не используются; это - прямые методы. Второе семейство использует первые производные функционала; такие методы обычно наз. методами спуска. Третью группу методов составляют алгоритмы с использованием вторых производных функционала.
В задачах минимизации функционалов, не обладающих свойством устойчивости, для построения последовательностей {zn}, сходящихся к элементу z*, применяют методы регуляризации.
Лит.:[1] Тихонов А. Н., Арсенин В. Я., Методы решения некорректных задач, М., 1974; [2] Сеа Ж., Оптимизация. Теория и алгоритмы, пер. с франц., М., 1973.
Ю. В. Ракитский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
