МЕТАТЕОРИЯ

- совокупность математич. средств и методов, предназначенных для описания и определения нек-рой формальной аксиоматич. теории, а также для исследования ее свойств. М. является важной составной частью метода формализации - одного из центральных методов математич. логики.

Суть этого метода можно кратко охарактеризовать следующим образом. Допустим, нас интересует нек-рая содержательная математич. теория T₁. Это может быть сложная теория, семантика к-рой недостаточно интуитивно ясна (напр., это может быть теория множеств, математич. анализ, арифметика 2-го порядка и т. п.). Нас интересует, является ли Т ₁ непротиворечивой теорией или совместен ли с Т ₁ нек-рый математич. принцип (напр., выбора аксиома). С целью выяснения этого вопроса вначале формулируется точный логико-математич. язык Q такой, что все интересующие пас утверждения Т ₁ записываются в виде формул языка Q. Затем логич. принципы, употреблявшиеся в теории для получения новых фактов, формализуются в виде аксиом и чисто формальных правил вывода, позволяющих выводить новые формулы языка Qиз аксиом и уже выведенных формул. Таким образом, возникает формальная система (или, иначе, формальная аксиоматическая теория, исчисление) точно описывающая нек-рый интересующий, нас фрагмент содержательной теории Т ₁. Существенно при этом, что формулировка не требует исчерпывающего проникновения в, быть может, весьма сложную семантику Т ₁. Исчисление строится по простым законам как чисто знаковая система и для понимания устройства этой знаковой системы нет нужды вникать в смысл выводимых в ней формул.

Такой подход открывает, во-первых, возможность строго математически сформулировать интересующие нас проблемы, относящиеся к выводимости нек-рых формул в и, во-вторых, исследовать 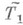средствами нек-рой содержательной теории Т ₂. В этой ситуации 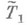наз. предметной теорией, а Т ₂- ее метатеорией.

С точки зрения оснований математики важно, чтобы Т ₂ была в нек-ром отношении более надежной теорией, чем Т ₁ , так что исследование средствами Т ₂ можно было бы рассматривать как действительное разъяснение и обоснование неясных деталей семантики Т ₁ с помощью более убедительной теории Т ₂ . В этой связи особенное предпочтение отдается достаточно надежным М., отражающим финитные установки в математике, теориям, построенным в рамках интуиционизма или конструктивной математики. Впрочем, вне оснований математики это ограничение не является обязательным. Если нас интересует не столько вопрос об интуитивной ясности Т ₁, сколько просто факт о выводимости или невыводимости нек-рых формул в 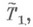естественно исследовать 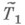средствами любой исторически сложившейся и убедительной для исследователя математич. теории Т ₂, не накладывая никаких априорных ограничений.

Можно далее исследовать аналогичным образом и метатеорию Т ₂ , построив формальную систему 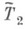и изучая уже 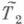средствами нек-рой метамета-теории Т ₃ . Такого рода исследования характерны для доказательств теории.

Лит.:[1] Клини С. К., Введение в метаматематику, пер. С англ., М., 1957.

А. Г. <Драгалин