- АСИМПТОТА
кривой
 , имеющей бесконечную ветвь,- прямая, обладающая тем свойством, что расстояние от точки
, имеющей бесконечную ветвь,- прямая, обладающая тем свойством, что расстояние от точки  кривой до этой прямой стремится к нулю при движении ее вдоль ветви к бесконечностп. А. может быть вертикальной или наклонной. Вертикальная А. имеет уравнение
кривой до этой прямой стремится к нулю при движении ее вдоль ветви к бесконечностп. А. может быть вертикальной или наклонной. Вертикальная А. имеет уравнение 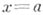 , причем
, причем  при
при  (односторонне). Для существования наклонной А., имеющей уравнение
(односторонне). Для существования наклонной А., имеющей уравнение 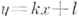 , необходимо и достаточно, чтобы существовали пределы .
, необходимо и достаточно, чтобы существовали пределы .
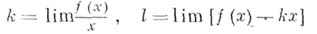
при
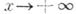 (или при
(или при  ).
).
Аналогичные формулы получаются и при параметрнч. задании кривой. В полярных координатах А. кривой
 , где
, где 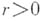 , с углом наклона
, с углом наклона 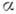 , определяется условием
, определяется условием 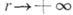 при
при  . Расстояние
. Расстояние  этой А. от начала координат вычисляется по формуле:
этой А. от начала координат вычисляется по формуле: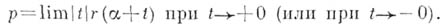
Если вдоль бесконечной ветви кривой существует предельное положение касательной, то оно есть А. Обратное не всегда верно. Напр., кривая
 имеет при
имеет при  асимптоту
асимптоту 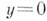 , хотя предельного положения касательной не существует. Среди кривых 2-го порядка А. имеют только гиперболы. А. гиперболы
, хотя предельного положения касательной не существует. Среди кривых 2-го порядка А. имеют только гиперболы. А. гиперболы  определяются уравнениями
определяются уравнениями 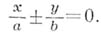 Наклонная А. дает простое - линейное по х - асимптотическое приближение функции
Наклонная А. дает простое - линейное по х - асимптотическое приближение функции
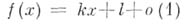
при
 (или при
(или при 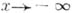 ).
).
Лит.:[1] Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; [2] Кудрявцев Л. Д., Математический анализ, т. 1, 2 изд., М., 1973. Л. П. Купцов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
