КРИСТОФФЕЛЯ ЧИСЛА,

Кристоффеля коэффициенты,- коэффициенты квадратурной формулы

точной для алгебраич. многочленов степени 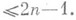Узлы 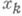такой квадратурной формулы являются нулями многочлена степени n, ортогонального на [ а, Ь]относительно распределения 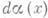всем многочленам степени га-1; если то К. ч. определяются однозначно. К. ч. и

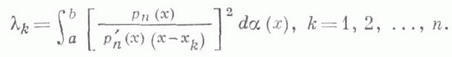
Если многочлены ортонормированны, то К. ч. представимы в виде

где К _n - старший коэффициент многочлена

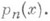
В случае а= - 1, b=1 и 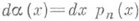являются Ле жандра многочленами., а К. ч.

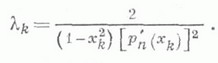
Эти выражения указаны Э. Кристоффелем [1]. Для n=1, 2, ... ,7 эти коэффициенты были вычислены К. Гауссом (С. Gauss). См. также Гаусса квадратурная формула.

Лит.:[1] Christoffel Е. В., "J. reine und angew. Math.", 1858, Bd 55, S. 61-82; [2] Ceгё Г., Ортогональные многочлены, пер. с англ., М., 1962; [3] Натансон И. П., Конструктивная теория функций, М.- Л., 1949. Н. И. Корнейчук, В. Л. Моторный.