- КОСМОЛОГИЧЕСКАЯ ПОСТОЯННАЯ
физическая постоянная, характеризующая свойства вакуума, к-рая иногда вводится в общей теории относительности. С учетом К. п. уравнения Эйнштейна имеют вид

где L - К. п., gij - метрический тензор, Rij- тензор Риччи, R- кривизна пространства, Tij - тензор энергии-импульса, с - скорость света, G - гравитационная постоянная. Эти уравнения являются уравнениями Лагранжа для действия

где S0 - действие для вещества, V- четырехмерный объем. К. п. была введена в общую теорию относительности [1] для того, чтобы уравнения гравитационного поля допускали пространственно однородное статическое решение (так. наз. космологическая модель Эйнштейна). После построения теории эволюционирующей космологич. модели Фридмана и получения ее наблюдательных подтверждений, отсутствие такого решения у исходных уравнений Эйнштейна не рассматривается как недостаток теории. Достоверных указаний на отличие К. п. от нуля нет. Однако наличие достаточно малой К. п.
 не противоречит наблюдательным данным и общим физическим принципам.
не противоречит наблюдательным данным и общим физическим принципам.
Наличие К. п. может существенно изменять некоторые этапы эволюции наиболее распространенных космологич. моделей (см. [2]). В связи с этим космологич. модели с К. п. предлагалось использовать для объяснения нек-рых свойств распределения квазаров (см. [3], [4], [5]).
Член
 в уравнениях гравитационного поля можно включить в тензор энергии-импульса и рассматривать как тензор энергии импульса вакуума (см. [2]). В этом случае вакуум имеет плотность энергии
в уравнениях гравитационного поля можно включить в тензор энергии-импульса и рассматривать как тензор энергии импульса вакуума (см. [2]). В этом случае вакуум имеет плотность энергии  и давление
и давление  что соответствует уравнению состояния
что соответствует уравнению состояния  В теории с К. п. свойства вакуума сказываются уже в нерелятивистском приближении. Так, гравитационный потенциал точечной массы в теории с К. п. равен (см. [6]):
В теории с К. п. свойства вакуума сказываются уже в нерелятивистском приближении. Так, гравитационный потенциал точечной массы в теории с К. п. равен (см. [6]):
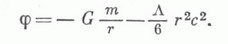
Член
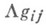 инвариантен по отношению к преобразованиям локальной группы Лоренца, что соответствует принципу лоренц-инвариантности вакуума в квантовой теории поля. Представление о К. п. как о величине, характеризующей плотность энергии и давление вакуума, в принципе позволяет связать представление о К. п. с представлениями квантовой теории поля. Имеется ряд формул, связывающих значение К. п. с фундаментальными физическими постоянными и возрастом Вселенной (см. [2]).
инвариантен по отношению к преобразованиям локальной группы Лоренца, что соответствует принципу лоренц-инвариантности вакуума в квантовой теории поля. Представление о К. п. как о величине, характеризующей плотность энергии и давление вакуума, в принципе позволяет связать представление о К. п. с представлениями квантовой теории поля. Имеется ряд формул, связывающих значение К. п. с фундаментальными физическими постоянными и возрастом Вселенной (см. [2]).
Лит.:[1] Эйнштейн А., Собр. научных трудов, т. 1, М., 1965, с. 601-12; [2] Зельдович Я. Б., Новиков И. Д., Строение и эволюция Вселенной, М., 1975; [3] РеtrosianV., SalpeterE., SzekeresP., "Astrophys. J.", 1967, v. 147, p. 1222-26; [4] Шкловский И. С., "Астрономический циркуляр", 1967, Ni429; [5] Кардашёв Н. С., там же, Л 430; [6] Толмен Р., Относительность, термодинамика и космология, пер. с англ., М., 1974. Д. Д. Соколов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
