КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВО
- КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВО
алгебраического многообразия - конечное объединение локально замкнутых (в Зариского топологии )подмножеств. Локально замкнутым подмножеством наз. пересечение открытого и замкнутого подмножеств. К. п. образуют булеву алгебру и могут быть определены как элементы булевой алгебры, порожденной алгебраич. подмногообразиями. Роль К. п. в алгебраич. геометрии объясняет следующая теорема ГОевалле: если 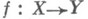 - морфизм алгебраич. многообразий, то f(X)(и более того, образ любого К. п. из X)является К. п. в У. С этим фактом связано то, что "алгебраические" условия выделяют конструктивные подмножества алгебраич. многообразий.
- морфизм алгебраич. многообразий, то f(X)(и более того, образ любого К. п. из X)является К. п. в У. С этим фактом связано то, что "алгебраические" условия выделяют конструктивные подмножества алгебраич. многообразий.
Отображение h: наз. конструктивным, если h{X )конечно и для любой точки
наз. конструктивным, если h{X )конечно и для любой точки  прообраз A-1(i) есть К. п. в X.
прообраз A-1(i) есть К. п. в X.
Лит.:[1] Grothendieck A., Elements de geometrie algebrique, t. 4, P., 1964; [2] Борель А., Линейные алгебраические группы, пер. с англ., М., 1972.
В. И. Данилов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "КОНСТРУКТИВНОЕ ПОДМНОЖЕСТВО" в других словарях:
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
ИНТЕРПОЛИРОВАНИЕ — интерполяция, в простейшем, классическом смысле конструктивное восстановление (быть может, приближенное) функции определенного класса по известным ее значениям или значениям ее производных в данных точках. Пусть даны n+l точек сегмента D=[ а, b] … Математическая энциклопедия
Упорядоченное поле — алгебраическое поле, для всех элементов которого определён линейный порядок, согласованный с операциями поля. Наиболее практически важными примерами являются поля рациональных и вещественных чисел. Термин впервые предложил Эмиль Артин в 1927 г.… … Википедия
Алгоритмов теория — раздел математики, изучающий общие свойства Алгоритмов. Содержательные явления, приведшие к образованию понятия «алгоритм», прослеживаются в математике в течение всего времени её существования. Однако само это понятие сформировалось лишь… … Большая советская энциклопедия
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
КОНСТРУКТИВНЫХ МОДЕЛЕЙ ТЕОРИЯ — один из разделов математики, возникший на границе моделей теории, алгебры и теории рекурсивных функций и связанный с изучением вопросов эффективности в моделях и алгебрах. Статья А. И. Мальцева Конструктивные алгебры [1] явилась первой обзорной… … Математическая энциклопедия
ВЫНУЖДЕНИЯ МЕТОД — форсинг метод, особый способ доказательства существования моделей аксиоматич. теорий, предложенный П. Козном в 1963 для доказательства совместимости отрицания континуум гипотезы щСН и других теоретико множественных предложений с аксиомами системы … Математическая энциклопедия
ФУНКЦИЯ — (лат. functio – исполнение) обязанность, круг деятельности. «Функция – это существование, мыслимое нами в действии» (Гёте). Наука о функциях органов живых существ – физиология; специальная наука о функциях нервной системы – физиология органов… … Философская энциклопедия
ПОРЯДКА ОТНОШЕНИЕ — бинарное (двуместное, двучленное) отношение, обладающее свойствами иррефлек сивности (см. Рефлексивность) и транзитивности (из чего следует также его антисимметричность, см. Симметричность). П. о. упорядочивает элементы множества, на к ром оно… … Философская энциклопедия
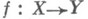 - морфизм алгебраич. многообразий, то f(X)(и более того, образ любого К. п. из X)является К. п. в У. С этим фактом связано то, что "алгебраические" условия выделяют конструктивные подмножества алгебраич. многообразий.
- морфизм алгебраич. многообразий, то f(X)(и более того, образ любого К. п. из X)является К. п. в У. С этим фактом связано то, что "алгебраические" условия выделяют конструктивные подмножества алгебраич. многообразий. наз. конструктивным, если h{X )конечно и для любой точки
наз. конструктивным, если h{X )конечно и для любой точки  прообраз A-1(i) есть К. п. в X.
прообраз A-1(i) есть К. п. в X.