- КОЛЬЦОИД
- обобщение понятия ассоциативного кольца. Пусть
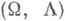 - многообразие универсальных алгебр сигнатуры Q. Алгебра
- многообразие универсальных алгебр сигнатуры Q. Алгебра  наз. кольцоидом над алгеброй G+ многообразия
наз. кольцоидом над алгеброй G+ многообразия 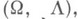 или
или 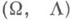 -кольцоидом, если G+={G, W} принадлежит многообразию
-кольцоидом, если G+={G, W} принадлежит многообразию  по умножению
по умножению 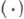 алгебра Gявляется полугруппой и выполняется закон дистрибутивности на втором месте относительно умножения
алгебра Gявляется полугруппой и выполняется закон дистрибутивности на втором месте относительно умножения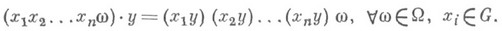
Операции из Q наз. аддитивными операциями кольцоида G,a G+ -аддитивной алгеброй кольцоида. К. наз. дистрибутивным, если законы дистрибутивности выполняются также и на первом месте, т. е.:
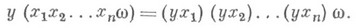
Обычное ассоциативное кольцо Gесть дистрибутивный К. над абелевой группой (и G+ - аддитивная группа кольца G). К. над группой наз. почти кольцом, К. над полугруппой - полукольцом, К. над лупой - неокольцом. Рассматривались также (под разными названиями, одно из которых - менгерова алгебра) К. над кольцами.
Лит.:[1] Курош А. Г., Общая алгебра, лекции 1969- 1970 учебного года, М., 1974.
О. А. Иванова.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
