КВАЗИСИМПЛЕКТИЧЕСКОЕ ПРОСТРАНСТВО

- нечетномерное проективное пространство Р _2п-1, в к-ром заданы нульсистемы:

и

Первая нульсистема переводит точки пространства в гиперплоскости, проходящие через (2n-2m-1)-плоскость вторая нульсистема - в точки этой же плоскости.

Плоскость х ^а=х ^т+а= 0 наз. абсолютной, а обе нуль-системы - абсолютными нульсистемами К. п.

К. п. является частным случаем полусимплектических пространств.

Коллинеации пространствапереводящие в себя абсолютную плоскость, имеют вид:

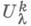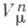и матрицы и - симплектич. матрицы порядков 2т и (2п-2m); 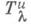- прямоугольная матрица с 2m столбцами и (2n-2т )строками.

Эти коллинеации наз. квазисимплект и чески ми преобразованиями пространства S^2m-1_P2n-1. Они перестановочны с заданными нульсистемами пространства. Квазисимплектич. инвариант двух прямых определяется по аналогии с симплектич. инвариантом прямых симплектического пространства.

К. п.может быть получено из симплектического путем предельного перехода от абсолюта пространства к абсолюту пространства

Именно, первая из заданных нульсистем переводит все точки пространства в плоскости, проходящие через абсолютную плоскость, а вторая - переводит все плоскости в точки той же плоскости.

Квазисимплектич. преобразования образуют группу, являющуюся группой Ли.

Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969.

Л. А. Сидоров.