ДЬЁДОННЕ МОДУЛЬ

- модуль Мнад кольцом Витта векторов W(k), где к- совершенное поле характеристики р>0, снабженный двумя эндоморфизмами F_M и V_M, удовлетворяющими следующим соотношениям:

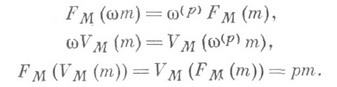
Здесь w=(а ₀, ..., а _n, ...)W(k), w^(p)=(a^p₀, ..., a^p_n, ...). Эквивалентное определение состоит в том, что Месть левый модуль над кольцом D_k (кольцом Дьёдонне), порожденным W(k)и двумя переменными Fи Vсвязанными соотношениями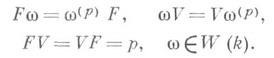

Для любого целого n>0 существует изоморфизм

где D_kVⁿ- левый идеал, порожденный Vⁿ,a W_nk- усеченная k-схема Витта. Д. м. играют важную роль в классификации унинотентных коммутативных алгебраических групп (см. [1]). Д. м. наз. также левые модули над пополнением D_k кольца D_k относительно топологии, порождаемой степенями двустороннего идеала {F, V )кольца D_k.

Лит.:[1] Dieudоnne J., "Аmеr. J. Math.", 1957, v. 79, №2 p. 331-88; [2]Demazure M., Gabriel P., Groupes algebriques, t.1, P.-Amst., 1970; [3] Mанин Ю. И., "Успехи чатем. наук", 1963, т. 18, в. 6, с. 3-90.

И. В. Долгачев.