ДРЕЙФОВЫЕ УРАВНЕНИЯ

- приближенные уравнения движения заряженной частицы в электрическом и магнитном полях, полученные с помощью усреднения по быстрому вращению частицы под действием магнитного поля. Д. у. справедливы в том случае, когда магнитное поле Вмедленно меняется в пространстве и во времени, а электрич. поле Емало по сравнению с магнитным:

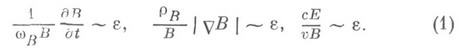
Здесь е - малый параметр, w_B=еВ/тс- ларморовскаячастота,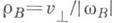- ларморовский радиус, v- величина скорости частицы, - составляющая скорости в направлении, перпендикулярном магнитному полю. Д. у. получаются из полных уравнений движения разложением по степеням 8 при помощи метода усреднения [1]. Они имеют следующий вид:

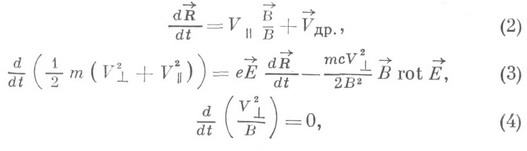
где

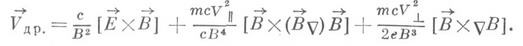
Система (2) - (4), называемая дрейфовой системой, записана относительно вспомогательных усредненных переменных связанных с исходными переменными 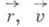определенными соотношениями. Дрейфовая скорость V _др, в уравнении (2) описывает медленное движение по усредненной траектории в направлении, перпендикулярном магнитному полю:

Уравнения (3), (4) имеют второй порядок точности по e и определяют величины 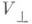и 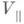с точностью до членов первого порядка в течение промежутка времени t, содержащего много ларморовских периодов 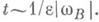Уравнение (2) имеет первый порядок точности по е.

Величина к-рая представляет собой интеграл дрейфовой системы (2) - (4), является приближенным интегралом истинного движения. Она наз. адиабатическим инвариантом. В статическом случае, когда и 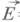= 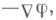уравнение (3) допускает интеграл энергии

для усредненного движения.

Возможно обобщение дрейфовой системы на релятивистский случай (см. [2], [3]).

Лит.:[1] Боголюбов Н. Н., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 3 изд., М., 1963; [2] Сивухин Д. В., в кн.: Вопросы теории плазмы, в. 1, М., 1963, с. 7-97; [3] Морозов А. И., Соловьев Л. С, там те, в. 2, М., 1963, с. 177-261.

Д. П. Костомаров.