ГЮЙГЕНСА ПРИНЦИП

утверждение, в силу к-рого при распространении колебаний, описываемом волновым уравнением в пространстве нечетного числа измерений, резко локализованное начальное состояние наблюдается позднее в другой точке, как явление, столь же резко ограниченное. В случае четного числа пространственных переменных Г. н. не имеет места - сигнал от локализованного начального возмущения, принятый в точке наблюдения, будет размытым. Г. п. был впервые сформулирован X. Гюйгенсом (Ch. Huygens) в 1678 (см. [1]), а затем развит А. Френелем (A. Fresnel) в 1818 при исследовании проблем дифракции.

Г. п. является следствием математич. факта, что решение волнового уравнения в точке Мтрехмерного пространства в момент tвыражается через значения решения и его производных на произвольной замкнутой поверхности, содержащей точку Мвнутри, в предшествующие моменты времени. В частности, решение в точке ( М, t )задачи Коши для волнового уравнения определяется начальными данными только на пересечении начального многообразия с характеристич. конусом точки ( М, t).и не зависит от начальных данных внутри характеристич. конуса. Впервые строгая математич. формулировка Г. п. была дана Г. Гельмгольцем (Н. Hel-mholtz) в 1859 для стационарного и Г. Кирхгофом (G. Kirchhoff) в 1882 для нестационарного случаев.

Обобщением Г. п. на линейные гиперболич. уравнения 2-го порядка

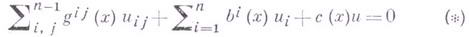
являются результаты Ж. Адамара (см. [2]), в силу к-рых решение задачи Коши для уравнения (*) при четных зависит лишь от начальных данных на пересечении начального многообразия с характеристич. коноидом тогда и только тогда, когда в фундаментальном решении (*) отсутствуют логарифмич. члены. Об описании всего класса уравнений вида (*), для к-рых справедлив Г. п., см. [4].

Лит.:[1] Гюйгенс X., Трактат о свете, пер. с франц., М.-Л., 1935; [2] Hadamard J., Lectures on Cauchy's problem in linear partial differential equations, New Haven-L., 1923; [3] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [4] Ибрагимов Н. X., Принцип Гюйгенса, в кн.; Некоторые проблемы математики и механики, Л., 1970. А. Г. Свешников.